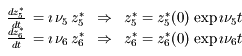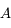 est diagonalisable donc il existe une matrice
est diagonalisable donc il existe une matrice 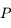 tel que:
tel que:
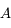 est diagonalisable donc il existe une matrice
est diagonalisable donc il existe une matrice 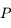 tel que:
tel que:
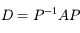 avec
avec 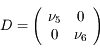
On définit le changement de variables: 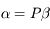
Le système devient alors: 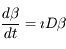
En notant 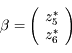 , le système est trivialement intégrable:
, le système est trivialement intégrable: