

Ex: Lever et coucher du Soleil |
Difficulté : ☆☆ Temps : 1h
Soit les repères orthonormés suivants :
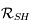 le repère
le repère 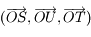 , où
, où 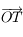 est perpendiculaire à
est perpendiculaire à 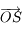 dans le plan
dans le plan 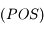 et tel que l'angle
et tel que l'angle 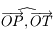 soit inférieur à
soit inférieur à 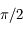 en valeur absolue et
en valeur absolue et 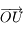 complète un repère orthonormé direct.
complète un repère orthonormé direct.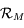 le repère
le repère 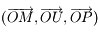 ,
, 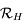 le repère
le repère 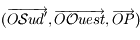 ,
,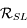 le repère
le repère 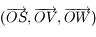 , où
, où 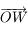 est perpendiculaire à
est perpendiculaire à 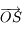 dans le plan
dans le plan 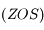 et tel que l'angle
et tel que l'angle 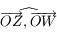 soit inférieur à
soit inférieur à 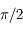 en valeur absolue et
en valeur absolue et 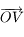 complète un repère orthonormé direct.
complète un repère orthonormé direct.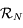 le repère
le repère 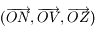 ,
,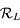 le repère
le repère 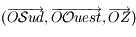 .
.Le but de l'exercice est d'établir relations entre les coordonnées horaires et coordonnées locales du Soleil en utilisant des matrices de rotation entre les différents repères.
Montrer que l'on passe du repère 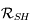 au repère
au repère 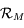 par une rotation d'angle
par une rotation d'angle 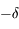 et d'axe
et d'axe 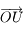 . Donner la matrice de passage
. Donner la matrice de passage 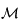 de la base de
de la base de 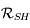 à celle de
à celle de 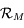 .
.
Montrer que l'on passe du repère 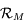 au repère
au repère 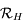 par une rotation d'angle
par une rotation d'angle 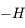 et d'axe
et d'axe 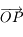 . Donner la matrice de passage
. Donner la matrice de passage 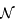 de la base de
de la base de 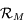 à celle de
à celle de 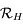 .
.
Montrer que l'on passe du repère 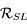 au repère
au repère 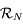 par une rotation d'angle
par une rotation d'angle 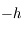 et d'axe
et d'axe 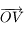 . Donner la matrice de passage
. Donner la matrice de passage 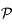 de la base de
de la base de 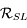 à celle de
à celle de 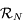 .
.
Montrer que l'on passe du repère 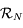 au repère
au repère 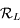 par une rotation d'angle
par une rotation d'angle 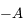 et d'axe
et d'axe 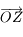 . Donner la matrice de passage
. Donner la matrice de passage  de la base de
de la base de 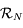 à celle de
à celle de 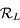 .
.
Montrer que l'on passe du repère 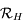 au repère
au repère 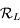 par une rotation d'angle
par une rotation d'angle 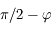 et d'axe
et d'axe 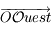 . Donner la matrice de passage
. Donner la matrice de passage 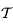 de la base de
de la base de 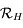 à celle de
à celle de 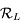 .
.
Ecrire les coordonnées de 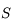 en fonction de
en fonction de 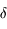 et
et 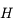 dans
dans 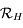 .
.
Ecrire les coordonnées de 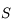 en fonction de
en fonction de 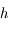 et
et 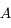 dans
dans 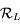 . Puis les coordonnées de
. Puis les coordonnées de 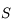 dans le repère
dans le repère 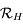 en fonction
de
en fonction
de 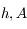 et
et 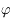 . En déduire trois relations, dépendant de
. En déduire trois relations, dépendant de 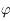 , entre les coordonnées horaires et les coordonnées locales du Soleil.
, entre les coordonnées horaires et les coordonnées locales du Soleil.
En déduire les valeurs de l'angle horaire 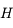 au moment du lever et du coucher du Soleil en fonction de
au moment du lever et du coucher du Soleil en fonction de 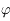 et
et 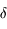 .
.
En déduire les valeurs de 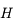 (mesuré entre -12h et +12h) et de la durée du jour au moment des équinoxes (
(mesuré entre -12h et +12h) et de la durée du jour au moment des équinoxes (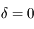 ), du solstice d'été
), du solstice d'été 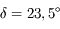 et du solstice d'hiver (
et du solstice d'hiver (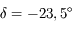 ) en un point de latitude
) en un point de latitude 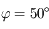 (approximativement la ville de Lille, France)
(approximativement la ville de Lille, France)