Auteur : Alain Vienne
On considère une sonde spatiale qui se déplace dans le système solaire. On suppose qu'elle ne subit que l'attraction gravitationnelle du Soleil 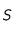 . Sous cette hypothèse, le mouvement de cette sonde autour du Soleil est un mouvement képlérien c'est-à-dire que la trajectoire est une conique dont le Soleil occupe l'un des foyers.
. Sous cette hypothèse, le mouvement de cette sonde autour du Soleil est un mouvement képlérien c'est-à-dire que la trajectoire est une conique dont le Soleil occupe l'un des foyers.
Les coniques sont des ellipses (comme le dit la première loi de Képler) ou des hyperboles ou des paraboles.
 Définition
Définition
Une conique est l'ensemble des points dont la somme ou la différence, des distances à 2 points fixes est constante. Ces 2 points sont appelés foyers et la distance constante est appelée grand axe
On ne considère pas ici le cas des paraboles qui est le cas limite entre les ellipses et les hyperboles. Une parabole peut être vue comme une ellipse dont l'un des foyer est rejeté à l'infini, ou symétriquement, comme une hyperbole dont l'un des foyers est rejeté à l'infini.
L'exercice proposé considère 2 points 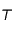 et
et 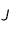 du système solaire avec
du système solaire avec 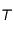 plus près de
plus près de 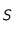 que
que 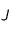 . On peut considérer que
. On peut considérer que 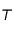 est la Terre et que
est la Terre et que 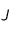 est Jupiter. Cela permet de fixer les idées mais il n'y a aucune obligation formelle à cela. On fait partir la sonde du point
est Jupiter. Cela permet de fixer les idées mais il n'y a aucune obligation formelle à cela. On fait partir la sonde du point 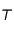 pour qu'elle arrive au point
pour qu'elle arrive au point 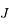 .
. 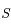 étant l'un des foyers, on note
étant l'un des foyers, on note 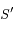 le second foyer de la conique
le second foyer de la conique 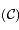 qui définit la trajectoire.
qui définit la trajectoire.

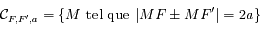 . Préciser le cas d'une ellipse et le cas d'une hyperbole. Pour ce dernier cas, préciser aussi comment sont distinguées les deux branches de l'hyperbole.
. Préciser le cas d'une ellipse et le cas d'une hyperbole. Pour ce dernier cas, préciser aussi comment sont distinguées les deux branches de l'hyperbole.
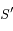 se trouve sur une hyperbole
se trouve sur une hyperbole 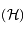 de foyers
de foyers 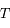 et
et 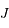 passant par
passant par 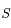
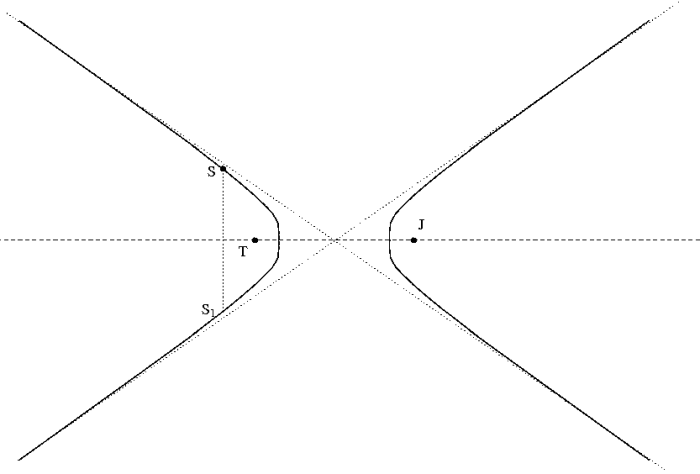
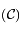 suivant la branche de
suivant la branche de 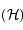 sur laquelle se trouve
sur laquelle se trouve 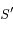 .
.
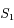 le point de
le point de 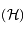 symétrique de
symétrique de 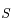 par rapport à l'axe focal.
par rapport à l'axe focal.
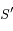 se trouve entre
se trouve entre 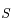 et
et 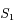 .
.
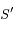 sur
sur 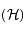 , exprimer le demi-grand axe
, exprimer le demi-grand axe 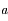 et l'
et l' de la conique
de la conique 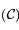 en fonction des distances entre les points
en fonction des distances entre les points 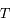 ,
, 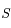 et
et 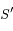
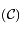 quand
quand
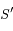 tend vers
tend vers 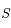
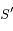 tend vers
tend vers 
 tend vers l'infini sur la même branche
tend vers l'infini sur la même branche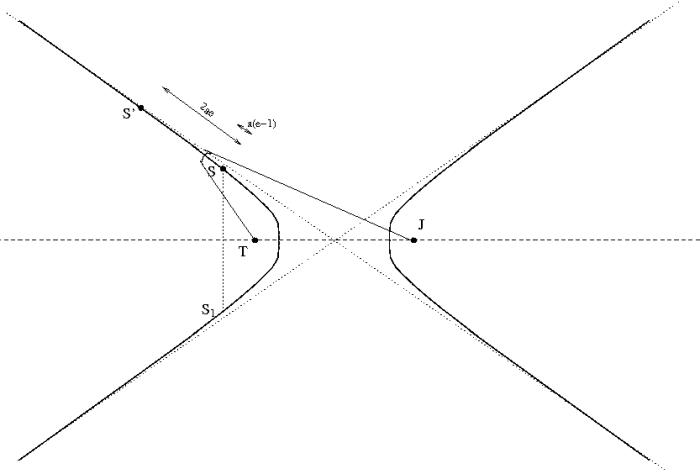
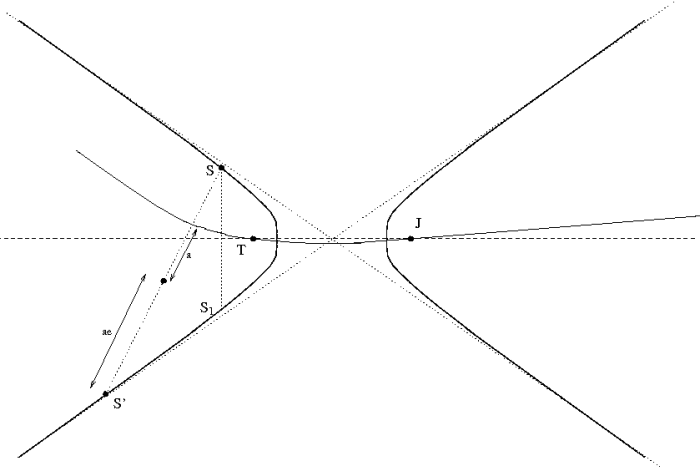
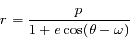
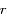 est la distance entre un corps
est la distance entre un corps 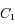 se trouvant à l'origine et le second corps
se trouvant à l'origine et le second corps 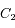 , et
, et 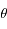 l'angle entre une direction de référence et le vecteur
l'angle entre une direction de référence et le vecteur 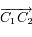 et
et  un nombre réel supérieur ou égale à zéro et
un nombre réel supérieur ou égale à zéro et 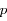 un nombre réel strictement supérieur à zéro.
un nombre réel strictement supérieur à zéro.
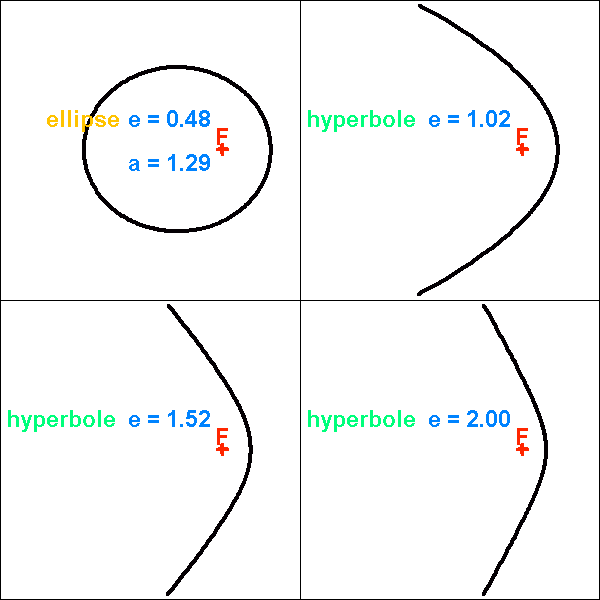
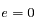 la solution est un cercle dont on déterminera le rayon.
la solution est un cercle dont on déterminera le rayon.
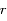 que l'on déterminera et que l'on notera
que l'on déterminera et que l'on notera 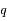 . La position pour laquelle cette distance est atteinte s'appelle le péricentre.
A quoi correspond
. La position pour laquelle cette distance est atteinte s'appelle le péricentre.
A quoi correspond 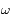 ?
Quand est-il pour le maximum de
?
Quand est-il pour le maximum de 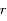 ? La position pour laquelle cette distance, notée
? La position pour laquelle cette distance, notée 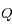 , est atteinte s'appelle apocentre lorsqu'elle existe.
, est atteinte s'appelle apocentre lorsqu'elle existe.
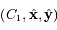 où l'axe des abscisses
où l'axe des abscisses 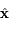 est dirigé vers le pericentre. Pour un point
est dirigé vers le pericentre. Pour un point 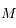 du plan on note
du plan on note 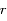 la distance
la distance 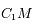 et
et 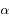 l'angle entre l'axe des abscisses et le vecteur
l'angle entre l'axe des abscisses et le vecteur 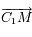 .
Ecrire l'équation de la
.
Ecrire l'équation de la 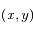 de
de 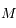 dans le repère
dans le repère 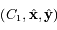 .On remarquera que l'équation obtenue est léquation générale d'une conique.
.On remarquera que l'équation obtenue est léquation générale d'une conique.
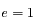 on obtient l'équation d'une parabole dont on déterminera les coordonnées du péricentre.
on obtient l'équation d'une parabole dont on déterminera les coordonnées du péricentre.
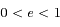 on obtient l'équation d'une ellipse dont on déterminera le centre, le demi-grand axe et le demi-petit axe.
on obtient l'équation d'une ellipse dont on déterminera le centre, le demi-grand axe et le demi-petit axe.
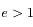 on obtient l'équation d'une hyperbole dont on déterminera le péricentre et les asymptotes.
on obtient l'équation d'une hyperbole dont on déterminera le péricentre et les asymptotes.
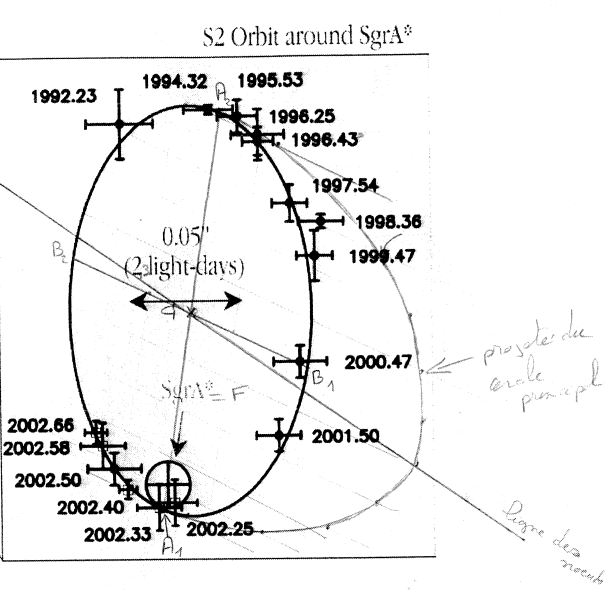
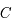 de l'ellipse projetée
de l'ellipse projetée
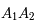
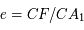 , puis
, puis 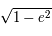 .
.
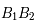 de
de 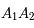 (donc le projeté du petit axe).
(donc le projeté du petit axe).
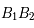 et de rapport
et de rapport 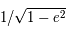 .
.
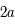 du grand axe de l'orbite réelle.
du grand axe de l'orbite réelle.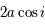 où
où 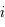 est l'inclinaison du plan de l'orbite avec le plan de projection.
est l'inclinaison du plan de l'orbite avec le plan de projection.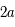 sur ce grand axe, puis convertir cette valeur en UA (
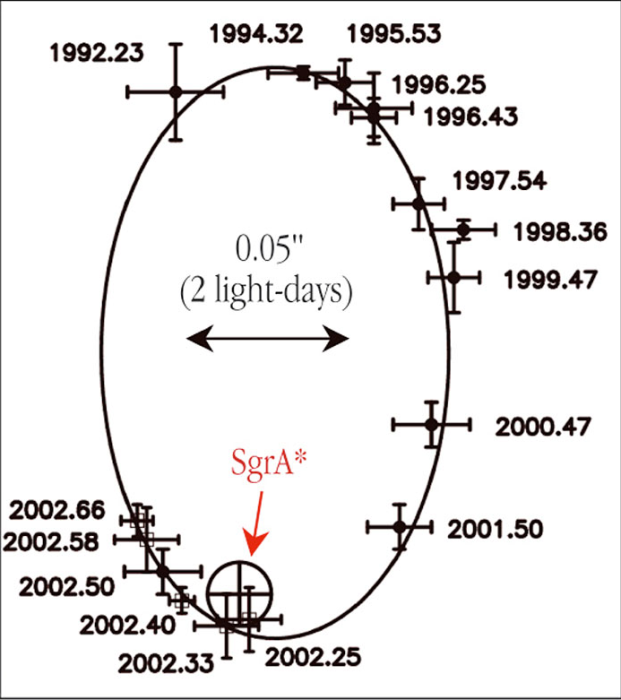
sur ce grand axe, puis convertir cette valeur en UA (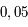 seconde de degré) et la distance du Soleil au centre de la Galaxie (26 000
seconde de degré) et la distance du Soleil au centre de la Galaxie (26 000 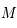 présente au foyer SgrA.
présente au foyer SgrA.
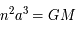 où
où 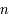 est la vitesse angulaire (
est la vitesse angulaire (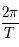 ), a le demi grand axe, M la masse et G une constante universelle (la constante de Gravitation).
), a le demi grand axe, M la masse et G une constante universelle (la constante de Gravitation).
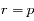 ce qui est bien l'équation d'un cercle de centre
ce qui est bien l'équation d'un cercle de centre 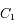 et de rayon
et de rayon 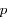 .
.
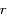 sera minimal quand
sera minimal quand 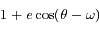 sera maximal, c'est à dire lorsque
sera maximal, c'est à dire lorsque ![\theta=\omega \,\,\,{\rm mod}\,[2\pi]](../pages_coniques/equations_coniques/equation62.png) . Dans ce cas on a
. Dans ce cas on a 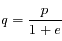 .
.
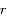 sera maximal quand
sera maximal quand 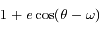 sera minimal, c'est-à-dire lorsque
sera minimal, c'est-à-dire lorsque ![\theta=\omega+\pi \,\,\,{\rm mod}\,[2\pi]](../pages_coniques/equations_coniques/equation66.png) . Or si
. Or si 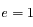 on s'aperçoit que dans ce cas
on s'aperçoit que dans ce cas 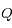 n'est pas défini, et si
n'est pas défini, et si 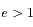 alors
alors 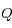 est négatif ce qui n'a pas de sens.
Lorsqu'il est défini (
est négatif ce qui n'a pas de sens.
Lorsqu'il est défini (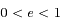 ), on a
), on a 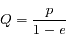 . On remarque que l'apocentre se trouve à l'opposé du péricentre.
. On remarque que l'apocentre se trouve à l'opposé du péricentre.
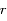 et
et 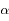 l'équation devient :
l'équation devient :
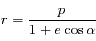 .
Avec
.
Avec 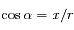 on a:
on a:
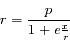 qui se transforme facilement en
qui se transforme facilement en 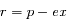 . On obtient finalement
. On obtient finalement
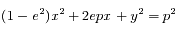 qui est l'équation d'une conique.
qui est l'équation d'une conique.
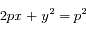 ,
,
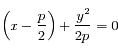 .
.
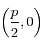 .
.
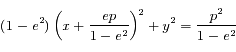 qui devient :
qui devient :
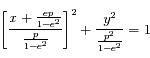
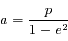 et
et 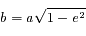 (qui est défini puisque
(qui est défini puisque 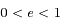 ), l'équation
devient:
), l'équation
devient:
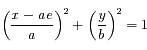
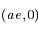 , de demi-grand axe
, de demi-grand axe 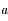 et de demi-petit axe
et de demi-petit axe 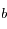 .
.
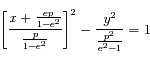
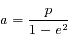 et
et 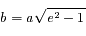 (qui est défini puisque cette fois
(qui est défini puisque cette fois 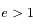 ). Ainsi l'équation devient:
). Ainsi l'équation devient:
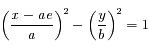
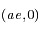 , et d'asymptotes :
, et d'asymptotes :
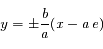 .
.
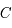 et par l'image du foyer
et par l'image du foyer 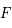 (c'est à dire la position indiquée de SgrA).
(c'est à dire la position indiquée de SgrA).
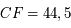 mm et
mm et 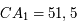 mm
mm
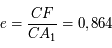
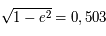 .
.
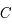 au milieu d'une corde parallèle à
au milieu d'une corde parallèle à 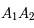 .
.
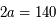 mm ce qui correspond à
mm ce qui correspond à 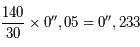
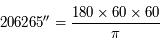 . Ce qui donne
. Ce qui donne 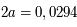 al
al 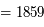 ua.
ua.
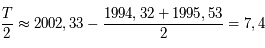 ans. Donc
ans. Donc 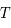 est estimée à
est estimée à 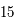 ans.
ans.
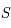 correspond au Soleil.
correspond au Soleil.
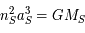 et
et 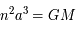 d'où
d'où 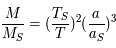
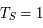 an et
an et 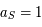 ua, donc
ua, donc 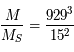 . Et donc
. Et donc 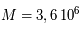 masses solaires.
masses solaires.