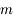 :
: 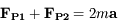 (les caractères en gras désignent des vecteurs)
(les caractères en gras désignent des vecteurs)
PFD appliqué au système des 2 masses 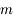 :
: 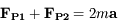 (les caractères en gras désignent des vecteurs)
(les caractères en gras désignent des vecteurs)
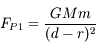 ,
, 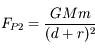
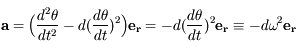 ,
,
où 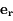 est un vecteur unitaire radial. On obtient alors :
est un vecteur unitaire radial. On obtient alors :
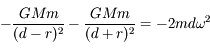
Au premier ordre en 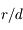 ,
, 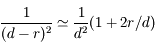 et
et 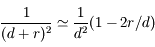
Donc 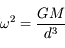 au premier ordre en
au premier ordre en 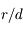 . On retrouve la troisième loi de Kepler.
. On retrouve la troisième loi de Kepler.