Ex: Pendule et équation de Mathieu

Auteurs: Arnaud Beck, Marc Fouchard, S. Renner, Florent Deleflie, Alain Vienne

Auteur: Alain Vienne

Exercice

Difficulté : ☆☆ Temps : 2h30

On considère l'équation différentielle suivante (équation de Mathieu):

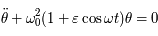
$\ddot{\theta} + \omega_0^2(1+\varepsilon \cos \omega t ) \theta = 0$

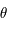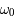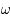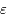Où $\theta$ est une fonction du temps . Cette équation dépend des paramètres $\omega_0$ , $\omega$ et $\varepsilon$ .

On souhaite déterminer dans quelles conditions la solution est bornée ou non.

Question 1)

Ecrire l'équation de Mathieu comme une équation différentielle du premier ordre:

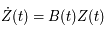
$\dot{Z}(t) = B(t) Z(t)$

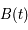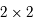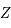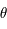où B(t) est une matrice $2 \times 2$ réelle. Donner la signification de la nouvelle inconnue (par rapport à $\theta$ ).

Solution

Question 2)

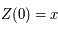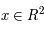On se donne une condition initiale Z(0) = x (on a $x \in \mathbb{R}^2$ ). D'après le théorème de Cauchy l'équation différentielle a alors une solution unique que l'on note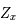 Z_x

Monter que l'application 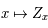$x \mapsto Z_x$ est linéaire.

Solution

Question 3)

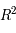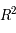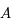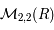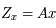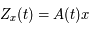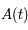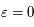Ainsi, à donné, cette application va de $\mathbb{R}^2$ dans $\mathbb{R}^2$ . Il existe donc une matrice de $\mathcal{M}_{2,2}(\mathbb{R})$ telle que Z_x = A x ou encore Z_x(t) = A(t) x . Explciter la matrice A(t) seulement dans le cas $\varepsilon = 0$ .

Solution

Question 4)

Pouvoir expliciter 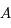, revient à obtenir toutes les solutions de l'équation différentielle. 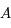est donc une inconnue. Montrer que 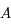vérifie le système suivant:

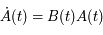
$\dot{A}(t) = B(t) A(t)$

A(0) = I

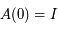
où 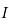est la matrice identité.

Solution

Question 5)

Montrer que pour tout système de la forme

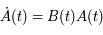
$\dot{A}(t) = B(t) A(t)$

, on a le résultat suivant:

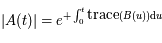
$| A(t) | = e^{ + \int_0^t \textrm{trace} (B(u)) \mathrm{d}u}$

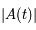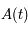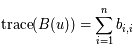où |A(t)| est le déterminant (d'ordre 2) de A(t) et $\textrm{trace} (B(u)) = \sum_{i=1}^n b_{i,i}$ (somme des éléments diagonaux).

Solution

Question 6)

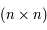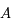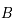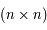Reprendre la question précédente, pour une système $(n\times n)$ . C'est-à-dire pour et étant des matrices $(n\times n)$ .

Solution

Question 7)

Montrer que:

$A(t+T) = A(t) \times A(T)$

où $T = \frac{2 \pi}{\omega}$

Solution

Question 8)

La matrice 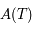A(T) s'appelle la matrice de Floquet.

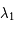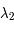Montrer que les valeurs propres $\lambda_1$ et $\lambda_2$ de la matrice de Floquet vérifient:

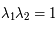
$\lambda_1 \lambda_2 = 1$

Solution

Question 9)

Ainsi, si ces valeurs propres sont réelles, l'une d'elle en valeur absolue est supérieure à 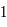. Donc avec 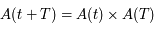$A(t+T) = A(t) \times A(T)$ et une condition initale prise dans la direction du vecteur propre associé à cette valeur propre, la solution tendera vers l'infini.

Montrer que sinon (valeurs propres complexes), les solutions sont bornées.

Solution

Question 10)

Dans notre cas (équation de Mathieu), 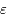$\varepsilon$ est petit. On peut alors montrer que la somme des valeurs propres de 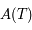A(T) est la trace de la matrice 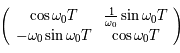$\left( \begin{array}{cc} \cos \omega_0 T & \frac{1}{\omega_0}\sin \omega_0 T \\ -\omega_0 \sin \omega_0 T & \cos \omega_0 T \end{array} \right)$ (ie: correspondant à celle trouvée dans le cas de perturbation nulle). Donc

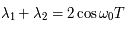
$\lambda_1 + \lambda_2 = 2 \cos \omega_0 T$

Montre que des solutions non bornées sont possibles que si la période du forçage est telle que

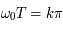
$\omega_0 T = k \pi$

où 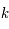est un entier relatif.

Solution