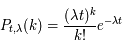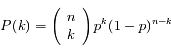
Le problème est équivalent à calculer la probabilité de trouver k occurrences de l'événement pour n tirages, la probabilité de réalisation durant chaque intervalle étant p = λt/n. La loi de Bernoulli donne :

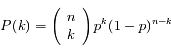
P(k) = \left ( \begin{array}{c} #n \\ #k \end{array} \right ) p^{k} (1-p)^{n-k}

Où 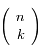\left ( \begin{array}{c} #n \\ #k \end{array} \right ) est le nombre de combinaisons de k éléments parmi n (notation standard moderne).

Pour passer à la limite continue, on prend n → ∞ en gardant pn = λt, et on remarque que :

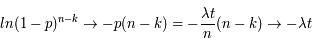
ln (1-p)^{n-k} \rightarrow -p (n-k) = -\frac{\lambda t}{n} (n-k) \rightarrow -\lambda t

Par ailleurs,

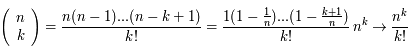
\left ( \begin{array}{c} #n \\ #k \end{array} \right ) = \frac{n(n-1)...(n-k+1)}{k!} = \frac{1(1-\frac{1}{n})...(1-\frac{k+1}{n})}{k!} \,n^k \rightarrow \frac{n^k}{k!}

Au total on trouve bien l'expression de la loi de Poisson :

P_{t,\lambda}(k)= \frac{(\lambda t)^k}{k!} e^{-\lambda t}