Ex: exposants de Lyapunov

Auteurs: S. Renner, Marc Fouchard

Auteur: Marc Fouchard

exposants de Lyapunov

Difficulté : ☆☆☆ Temps : 1h30

Question 1)

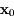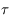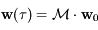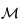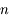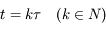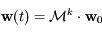Soit une orbite périodique de condition initiale ${\bf x}_0$ et de période $\tau$ . Ainsi après une période on a ${\bf w}(\tau)=\mathcal{M} \cdot {\bf w}_0$ , où $\mathcal{M}$ est une matrice carrée de dimension , et pour $t=k\tau \quad (k\in\mathbb{N})$ on a ${\bf w}(t)=\mathcal{M}^k \cdot {\bf w}_0$ . Montrer que si 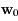${\bf w}_0$ est un vecteur propre de la matrice 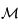$\mathcal M$ associé à la valeur propre 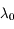$\lambda_0$ alors:

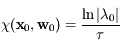
$\chi({\bf x}_0,{\bf w}_0)=\frac{\ln |\lambda_0|}{\tau}$

Solution

Question 2)

Ainsi on voit que pour les orbites périodiques les exposants de Lyapunov sont reliés au spectre, c'est-à-dire l'ensemble des valeurs propres, du Jacobien de 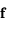$\bf f$ . Dans le cas général la matrice 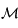$\mathcal M$ n'existe pas. Cependant on va voir qu'on peut définir un spectre d'exposants de Lypunov associé au Jacobien de 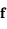${\bf f}$ ayant certaines similarités avec le spectre des valeurs propres d'une matrice.

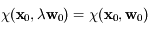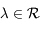Montrer que $\chi ({\bf x}_0,\lambda{\bf w}_0)=\chi({\bf x}_0,{\bf w}_0)$ , pour $\lambda \in \mathcal R$ .

Solution

Question 3)

Montrer que 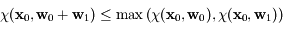$\chi({\bf x}_0,{\bf w}_0+{\bf w}_1})\le\max \left( \chi({\bf x}_0,{\bf w}_0),\chi({\bf x}_0,{\bf w}_1)\right)$ .

Solution

Question 4)

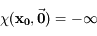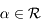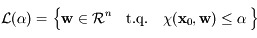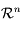Avec la convention $\chi({\bf x_0,\vec{\bf 0})=-\infty$ , montrer que pour tout $\alpha \in {\mathcal R}$ , l'ensemble $\mathcal{L}(\alpha)=\left\Big\lbrace {\bf w} \in {\mathcal R}^n \quad {\rm t.q.} \quad \chi({\bf x}_0,{\bf w})\le \alpha \right\Big\rbrace$ , forme un sous-espace vectoriel de $\mathcal{R}^n$ .

Solution

Question 5)

En déduire qu'il existe au plus exposants de Lyapunov distincts pour une trajectoire donnée.

Aide Solution

Remarque

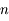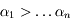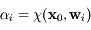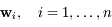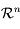On voit ainsi que les exposants de Lyapunov forment un spectre au même titre que les valeurs propres pour un opérateur linéaire. Si on a exposants distincts et tels que $\alpha_1>\dots\alpha_n$ , avec $\alpha_i=\chi({\bf x}_0,{\bf w}_i)$ , alors les vecteurs ${\bf w}_i, \quad i=1,\dots,n$ forment une base de $\mathcal{R}^n$ . Dans la pratique, on ne connait pas les vecteurs permettant de déterminer les exposants de Lyapunov. Mais si on prend un vecteur au hasard il apartiendra à 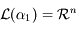$\mathcal{L}(\alpha_1)=\mathcal{R}^n$ mais peu probablement à 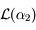$\mathcal{L}(\alpha_2)$ . En effet pour qu'il y appartienne il faudrait que la composante de ce vecteur suivant 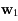${\bf w}_1$ soit égale à zéro. Lors d'un tirage au hasard cette probabilité est nulle.

Ainsi dans la pratique on calcule en général uniquement l'exposant maximal de Lyapunov 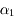$\alpha_1$ . Il permet de savoir si une orbite est stable ou chaotique. 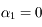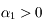En effet dans le cas d'une orbite stable la norme du vecteur tangent va très probablement augmenter linéairement avec le temps, ainsi $\alpha_1=0$ , alors que dans le cas chaotique elle va augmenter très probablement exponentiellement avec le temps, ainsi $\alpha_1>0$ .