Les parallaxes des étoiles proches

La première manière de déterminer la distance d'une étoile proche est de mesurer ce que l'on appelle sa parallaxe.

Parallaxe

Schéma montrant comment on définit la parallaxe d'une étoile

Crédit : G.B. Lima Neto, cours Université de São Paulo, Brésil

Parallaxe d'une étoile proche

Animation illustrant la notion de parallaxe : il s'agit de l'angle sous lequel depuis une étoile proche on verrait le rayon de l'orbite terrestre. L'image de droite montre la projection a 90° de celle de gauche, autrement dit le mouvement de l'étoile proche dans le plan du ciel. Echelles de distances dans l'Univers

Crédit : ASM

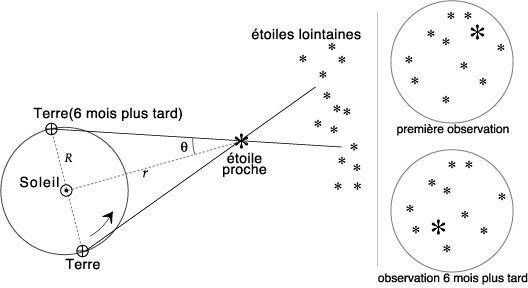
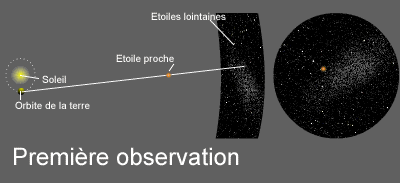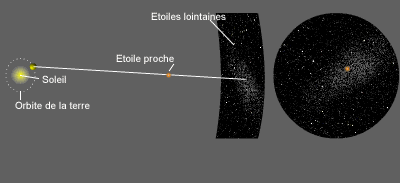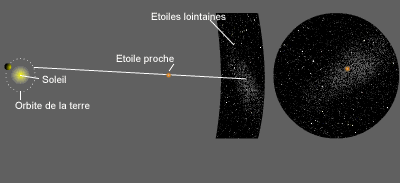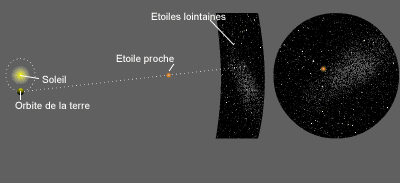
Lorsque la Terre est dans une certaine position, par exemple à l'équinoxe de printemps, elle voit l'étoile proche dans une certaine direction dans le ciel (par rapport à des étoiles lointaines). Six mois plus tard, à l'équinoxe d'automne, la même étoile semblera s'être déplacée par rapport aux étoiles lointaines (qui, elles, n'auront pas bougé). Si l'on connaît les propriétés optiques de l'ensemble télescope +caméra+détecteur, on peut estimer de quel angle sur le ciel l'étoile s'est déplacée par rapport aux étoiles lointaines et fixes d’arrière plan. On peut alors mesurer de combien l'étoile proche s'est déplacée par rapport aux étoiles lointaines et fixes d'arrière-plan.

Ainsi, connaissant les propriétés optiques de l'instrument utilisé (télescope + détecteur), on peut calculer la dimension du pixel en secondes d’angle (1 second d'arc vaut la 3600ème partie d'un degré d'angle). On peut donc mesurer 2 theta, où theta est la parallaxe de l'étoile (voir schéma ci-dessus).

On peut écrire : tan θ = ST / SE, et comme θ est un angle très petit on peut l'assimiler à sa tangente, à condition de le convertir en radians. D'où: θ (rad) = ST/SE. Comme on connaît ST (distance moyenne Terre-Soleil) et que l'on peut mesurer θ, on en déduit SE = distance de l’étoile au Soleil (ou à la Terre, la différence est minime).

La difficulté d'appliquer cette méthode est due au fait que les parallaxes θ sont des angles très petits, donc difficiles à mesurer, et seulement mesurables pour les étoiles proches. Au-delà les angles deviennent trop petits et impossibles à mesurer.

Le satellite Hipparcos a mesuré les parallaxes, et donc les distances d'environ 100.000 étoiles au début des années 1990, et le futur satellite Gaia devrait en mesurer dix fois plus d'ici quelques années. Il est très important de bien connaître la distance des étoiles, car il devient alors possible d'estimer leurs propriétés intrinsèques à partir des observations.