
|
On dispose de deux MHTI d'indice 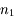 et
et 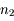 . Un rayon incident issu de
. Un rayon incident issu de 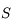 arrive sur le dioptre les séparant en
arrive sur le dioptre les séparant en 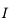 .
.
Le but de cette simulation est d'établir une loi liant l'angle incident et l'angle réfracté.
Nous venons de voir à la page précédente que :
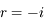
 .
.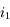 ,
, 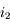 ,
, 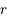 "
"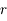 et
et 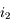 en fonction de
en fonction de 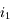
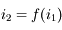 n'est clairement pas linéaire.
n'est clairement pas linéaire.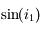 et
et 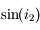
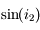 en fonction de
en fonction de 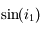
Lorsque les angles sont faibles, ils sont presque égaux à leur sinus (exprimé en radian). Donc lorsque 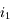 et
et 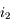 sont petits :
sont petits :
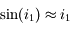
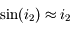
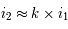
On retrouve le fait que la loi est presque linéaire pour les faibles angles.