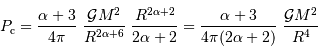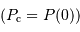 vers la surface
vers la surface 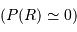 :
:
On cherche à intégrer la pression du centre 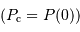 vers la surface
vers la surface 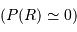 :
:
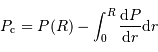
On suppose la pression de surface totalement négligeable. Il reste alors, en fonction de ce qui précède :
![P _{\mathrm{c}} = \int_0^R \rho g\ {\mathrm{d}} r = \int_0^R \beta r^\alpha \ { {\cal G} M \over R^{\alpha+3}} r^{\alpha+1} {\mathrm{d}} r = \beta { {\cal G} M \over R^{\alpha+3}} \int_0^R r^{2\alpha+1} {\mathrm{d}} r = {\alpha+3 \over 4\pi}\ { {\cal G} M^2 \over R^{2\alpha+6}} \left[ {r^{2\alpha+2}\over 2\alpha+2} \right]_0^R](../pages_physique-evolution/equations_pression-centrale/equation45.png)
L'expression du champ a conduit à la restriction 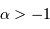 ; dans ce cas, la contribution en 0 ne diverge pas, et l'on trouve :
; dans ce cas, la contribution en 0 ne diverge pas, et l'on trouve :