Cette section propose des développements plus ardus, au-delà d'un programme de niveau L2 ou L3, mais bien utiles, concernant divers points d'optique.
- La notion d'étendue de faisceau permet, sans décrire complètement un faisceau, de connaître rapidement certaines propriétés spatiales.
- La diffraction par une pupille circulaire est établie en bonne et due forme.
- Une introduction à l'optique de Fourier est proposée.
- Les notions de cohérence temporelle et cohérence spatiale sont exposées.
- ...

Ça se complique.
Crédit :
ASM
Aberration de sphéricité
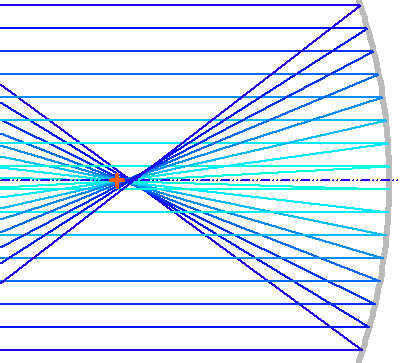
Programme de tracé de rayons.
Les rayons les plus éloignés de l'axe de révolution d'un miroir sphérique convergent plus près du miroir que les rayons paraxiaux. Des couleurs différentes sont utilisées uniquement pour permettent de distinguer les rayons entre eux.
Crédit :
ASM
Aberration sphérique
Un miroir sphérique est beaucoup plus simple à tailler qu'un miroir parabolique. Mais il ne rend pas les mêmes services, car il concentre la lumière imparfaitement ; plus le rayon est éloigné de l'axe optique, plus il va converger en avant du foyer. On parle d'aberration de sphéricité.
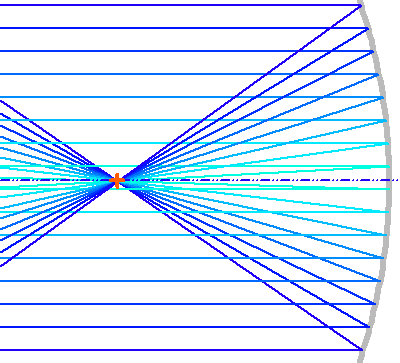
Contrairement au miroir sphérique, le miroir parabolique concentre parfaitement tous les rayons provenant d'un objet sur l'axe à l'infini.
Crédit :
ASM

Même pour un miroir parabolique, l'image d'un objet à l'infini hors axe n'est pas parfaitement ponctuelle. L'effet est analogue à l'aberration de sphéricité présentée par un miroir sphérique.
Crédit :
ASM
Aberration de coma
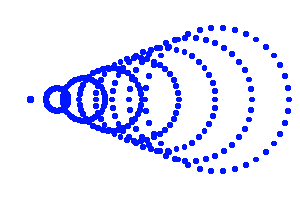
Diagramme de tracé de rayon montrant l'allure de la coma : l'image d'un point devient une petite tache allongée. comme une aigrette.
Crédit :
ASM
Coma
Un miroir parabolique est exempt de cette aberration de sphéricité, mais uniquement pour un objet centré sur l'axe et non hors axe . On parle dans ce cas d'aberration de coma, qui rend donc compte de l'aberration de sphéricité hors axe.
 Objectifs
Objectifs
Brièvement décrire les aberrations géométriques
Stigmatisme
La définition de la justesse de la formation d'image s'appelle le stigmatisme. Le stigmatisme idéal est atteint lorsque tous les rayons issus d'un point de l'objet convergent en un seul point de l'image.
Cette situation idéale n'est pas opérationnelle : il faut en pratique définir les conditions dans lesquelles la convergence est suffisante (p.ex. avec une précision dans le plan focal meilleure que la taille d'un pixel). Ces conditions sont d'autant mieux réalisées que l'on est proche de l'axe optique du système.
Aberration de coma
L'aberration de coma affecte tout rayon hors axe.
Crédit :
ASM
Distorsion
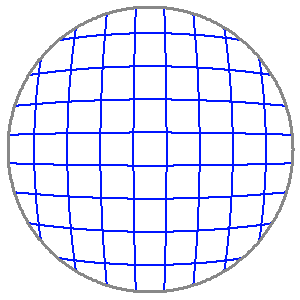
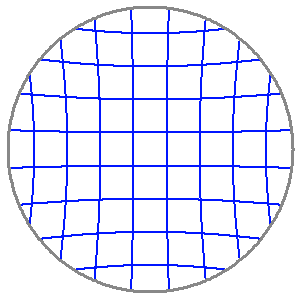
La distorsion transforme une grille rectangulaire en une grille en forme de barillet ou de coussinet.
Crédit :
ASM
Aberration chromatique
L'aberration chromatique apparaît pour une lentille simple, dont la focale dépend de la couleur.
Crédit :
ASM
Aberrations chromatiques
L'aberration chromatique apparaît pour une lentille simple : comme l'indice du matériau varie avec la longueur d'onde, la focale varie également. En règle générale, l'indice bleu, plus élevé donne une distance focale bleue plus courte.
Cette aberration est corrigée par l'utilisation de systèmes de lentilles (doublet, triplet...), avec des verres d'indices différents pour obtenir une focale équivalent quasiment identique pour toutes les longueurs d'onde considérées.
Les miroirs présentent l'avantage de ne pas induire d'aberrations
chromatiques (la lumière ne traverse pas le miroir). Leur
coefficient de réflexion, qui dépend intimement du traitement de
surface, est néanmoins chromatique.
Comparaison de diverses aberrations
Aberrations 
Les différents défauts géométriques cohabitent joyeusement, et les
distinguer n'est pas toujours facile, comme le montre le
diaporama ci-joint.
 Prérequis
Prérequis
Notion d'angle solide.
 Objectifs
Objectifs
Définir l'étendue de faisceau ; mais surtout montrer la conservation de l'étendue de faisceau.
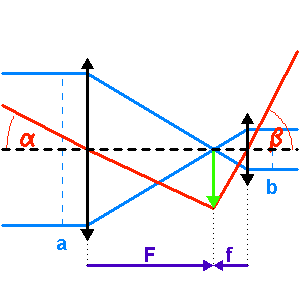
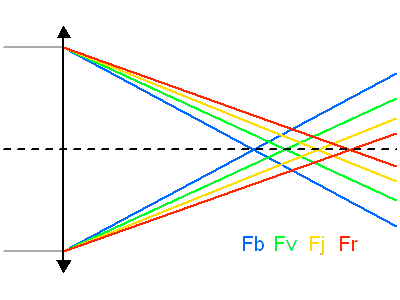
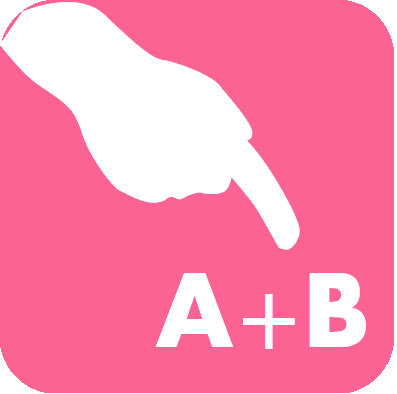
Le montage afocal transforme un faisceau de diamètre
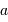
en un faisceau de diamètre
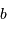
, avec un grossissement angulaire
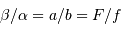
.
Crédit :
ASM
Exemple : montage afocal
Un montage afocal transforme un faisceau plan en un autre faisceau plan. Les rapports des diamètres des faisceaux et des inclinaisons en entrée et sortie sont intimement liés au grossissement.
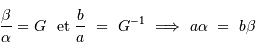
Le produit est un invariant, ce qui relate une relation physique plus générale : la conservation de l'énergie du faisceau.
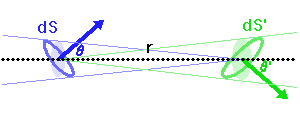
Conservation de l'étendue de faisceau, de l'élément émetteur
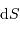
à l'aire collectrice
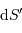
.
Crédit :
ASM
Faisceau, étendue de faisceau et conservation de l'énergie
La puissance (ou luminosité )
 transportée par un faisceau lumineux, émise par l'élément de surface S et reçue par S' se conserve (sorte de tautologie, le faisceau étant défini par l'ensemble des rayons lumineux, càd la totalité de la puissance lumineuse). Cette puissance est proportionnelle à la luminance
transportée par un faisceau lumineux, émise par l'élément de surface S et reçue par S' se conserve (sorte de tautologie, le faisceau étant défini par l'ensemble des rayons lumineux, càd la totalité de la puissance lumineuse). Cette puissance est proportionnelle à la luminance 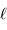 , à l'élément de surface émetteur et à l'élément d'angle solide d'émission.
, à l'élément de surface émetteur et à l'élément d'angle solide d'émission.
Un jeu d'écriture sur les grandeurs photométriques, avec les données de la figure, conduit à exprimer la conservation de la puissance lumineuse comme la conservation de l'étendue géométrique de faisceau. On définit cette étendue de faisceau, pour un faisceau traversant sans être collimaté (= sans perte d'énergie) un élément optique de section 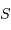 , occupant un angle solide
, occupant un angle solide 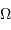 , dans un milieu d'indice unité (comme le vide ou comme l'air à peu de chose près), par le produit
, dans un milieu d'indice unité (comme le vide ou comme l'air à peu de chose près), par le produit 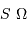 , qui se conserve le long du faisceau.
, qui se conserve le long du faisceau.
Pour les systèmes stigmatiques (càd, très grossièrement, donnant des images avec des aberrations limitées), la conservation de l'énergie se traduit par la conservation de l'étendue de
faisceau :
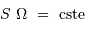
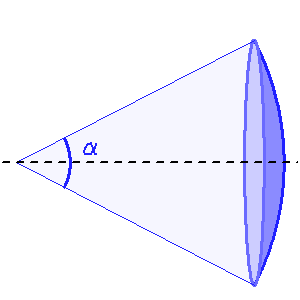
Faisceau divergeant d'une source quasi ponctuelle, collimaté : son énergie est localisée dans un cône.
Crédit :
ASM
Faisceau conique peu ouvert
Un faisceau conique d'ouverture totale 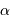 couvre un angle solide :
couvre un angle solide :
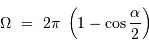
Si l'angle 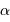 est petit, cet angle solide se réécrit simplement :
est petit, cet angle solide se réécrit simplement :
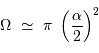
Au travers d'une optique de diamètre 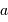 , la conservation du produit
, la conservation du produit 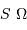 devient, pour ce faisceau conique :
devient, pour ce faisceau conique :
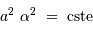
On retrouve donc le résultat obtenu dans le cadre du montage afocal.
Quelques conséquences
Comme conséquences importantes, on note que :
- Plus le faisceau collecté passe par un diamètre fin, plus il est divergent.
- Plus l'aire du collecteur est grande, plus l'étendue de faisceau est grande, plus les instruments doivent également être de grande taille pour offrir un grand diamètre au faisceau mis en forme.
- La surface du détecteur et l'angle solide qu'il peut voir (de l'ordre de l'angle d'ouverture du télescope) limitent nécessairement la taille angulaire du champ objet.
Etendue de faisceau cohérente
Un faisceau monochromatique est cohérent sur une étendue égale à 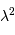 .
La justification est donnée en exercice.
.
La justification est donnée en exercice.
 Imagerie grand champ
Imagerie grand champ
Difficulté : ☆
Temps : 20 min
Le but d'une caméra est de réaliser un programme de cartographie, par imagerie grand champ. Les caractéristiques du détecteur sont fixées (taille du capteur CCD et caractéristiques de son optique), que l'on traduit par le produit 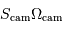 . Le but de l'exercice est de déterminer quel collecteur optimal utiliser pour réaliser ce programme.
. Le but de l'exercice est de déterminer quel collecteur optimal utiliser pour réaliser ce programme.
Question 1)
Comment varie la taille angulaire du champ objet en fonction de la surface 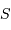 du collecteur ?
du collecteur ?
Se servir la conservation de l'étendue de faisceau
Question 2)
Le temps de pose est fixé par le rapport signal à bruit des observations, qui dépend essentiellement du nombre de photons collectés. Comment le temps de pose varie-t-il avec la surface du collecteur ?
Comment varie le nombre de photons collectés avec la surface collectrice ?
Question 3)
Y'a-t-il un intérêt particulier à utiliser un grand collecteur pour réaliser cette cartographie ? Quel usage peut-on conseiller à un télescope de la classe 4-m qui doit motiver son existence par rapport aux télescopes de nouvelle génération plus grands ?
Se servir des 2 questions précédentes.
Comparer la dépendance vis à vis de la surface collectrice 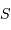 de la taille du champ élémentaire et du temps de pose élémentaire.
de la taille du champ élémentaire et du temps de pose élémentaire.
 Sur les 2 tableaux
Sur les 2 tableaux
Difficulté : ☆☆
Temps : 20 min

Le montage optique réel de CoRoT. Les 2 miroirs paraboliques hors-axe sont notés Primary mirror et M2. Lens correspond à l'optique de chambre ; Focal box aux détecteurs CCD.
Crédit :
CNES
CoRoT est un satellite du CNES lancé en décembre 2006, qui poursuit 2 objectifs scientifiques : la recherche d'exoplanètes par la méthode des transits d'une part, l'étude sismique de quelques étoiles de type solaire d'autre part. Ces 2 objectifs s'appuient sur la capacité de CoRoT à mener des observations de photométrie très précises. Le montage optique retenu consiste en l'association de 2 miroirs paraboliques confocaux (confocal  même foyer) hors axe, suivis par une optique de chambre conjuguant le faisceau issu des 2 paraboles avec le détecteur CCD. En pratique, pour les respecter les specifications de la formation d'image, cette optique de chambre est constituée de 6 lentilles.
même foyer) hors axe, suivis par une optique de chambre conjuguant le faisceau issu des 2 paraboles avec le détecteur CCD. En pratique, pour les respecter les specifications de la formation d'image, cette optique de chambre est constituée de 6 lentilles.
Question 1)
Faire à l'échelle un schéma de principe le plus simple possible du système équivalent à l'ensemble miroirs + optique de chambre avec 3 lentilles équivalentes pour respectivement les 2 miroirs et l'optique de chambre.
Revoir la page sur le montage afocal.
Question 2)
Le diamètre du premier miroir vaut 30 cm ; les focales des miroirs primaire et secondaire sont dans un rapport de 3 à 1. Que peut-on en déduire concernant les lentilles de l'optique de chambre ? En quoi consiste l'un des intérêts de ce montage ?
Revoir (encore !) la page sur le montage afocal.
Question 3)
Reprendre le schéma de principe, en respectant l'ouverture du faisceau à 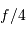 vu par la caméra, Calculer la focale
vu par la caméra, Calculer la focale 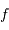 équivalente et la focale
équivalente et la focale 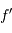 de l'optique de chambre.
de l'optique de chambre.
Question 4)
La question précédente met en évidence un gain sur l'optique de chambre. Mettre en évidence la contrainte associée, qui dérive de la conservation de l'étendue de faisceau. Conclure.
Simple application de la conservation de l'étendue de faisceau.
 Étendue cohérente
Étendue cohérente
Difficulté : ☆☆
Temps : 10 min
Un collecteur de diamètre 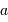 délivre une tache de diffraction d'ouverture (définie comme largeur à mi-hauteur)
délivre une tache de diffraction d'ouverture (définie comme largeur à mi-hauteur) 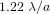 . On cherche à en déduire l'étendue de faisceau cohérente.
. On cherche à en déduire l'étendue de faisceau cohérente.
Question 1)
Justifier que l'étendue cohérente correspond au pic central de la diffraction.
Pourquoi le premier anneau de la tache de diffraction est-il noir? Que cela signifie-t-il ?
Question 2)
Déterminer l'étendue de faisceau cohérente. Montrer qu'elle est très voisine de
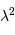 .
.
Revenir à la définition : exprimer 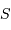 et
et 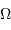 .
.
 D'un collecteur de 8 m à une fibre
D'un collecteur de 8 m à une fibre
Difficulté : ☆
Temps : 5 min
Un instrument du VLT (collecteur de diamètre 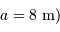 est alimenté par un faisceau de fibres de diamètre
est alimenté par un faisceau de fibres de diamètre 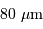 .
.
Question 1)
L'alimentation optimale de la fibre se fait à 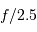 . En déduire l'ouverture angulaire du faisceau en entrée de fibre.
. En déduire l'ouverture angulaire du faisceau en entrée de fibre.
[1 points]
Question 2)
Que vaut le champ objet admissible sur le ciel ? L'exprimer en seconde d'angle.
[1 points]
 Observation au foyer et étendue de faisceau
Observation au foyer et étendue de faisceau
Difficulté : ☆☆
Temps : 15 min
On se propose de retrouver par l'application de la conservation de l'étendue de faisceau l'expression de la taille linéaire de l'image d'un objet à l'infini de diamètre angulaire 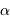 par un collecteur de diamètre
par un collecteur de diamètre 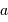 et de focale
et de focale 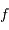 . On considère le seul cas où l'angle
. On considère le seul cas où l'angle 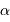 est petit. On note
est petit. On note 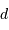 ladite taille linéaire.
ladite taille linéaire.
Question 1)
Exprimer le produit 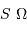 côté source, en fonction des données.
côté source, en fonction des données.
[1 points]
Question 2)
Rappeler l'expression de l'ouverture angulaire du collecteur, et exprimer le produit 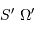 côté détecteur.
côté détecteur.
[2 points]
Question 3)
Exprimer la conservation de l'étendue de faisceau. Retrouve-t-on le résultat attendu ?
L'objet ayant une taille angulaire 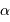 , quelle est la taille linéaire
, quelle est la taille linéaire 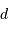 de son image.
de son image.
[2 points]
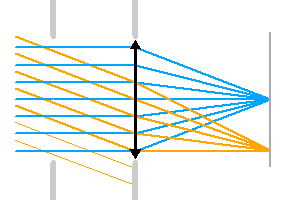
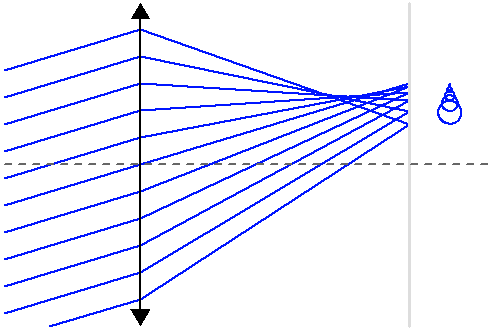
Illustration du phénomène de vignetage. Une partie du faisceau inclinés (en orange) est bloquée, alors que la totalité du faisceau d'incidence nulle (en bleu) est transmise : l'image sera moins lumineuse au bord.
Crédit :
ASM

Champ vigneté : les sources les plus éloignées se retrouvent éteintes.
Crédit :
ASM
Le vignetage
Le vignetage apparaît lorsque qu'un diaphragme coupe indûment le faisceau optique. Les bords de l'image ne sont alors plus suffisamment éclairés.
 Prérequis
Prérequis
Optique géométrique ; tracé de rayons.
 Objectifs
Objectifs
Bien accepter ou bien stopper les photons (sans trop rentrer dans les détails).
Champ et diaphragme
Le champ d'un instrument d'optique est la partie de l'espace dont cet instrument fournit une image acceptable.
Un diaphragme, c'est par définition ce qui limite un faisceau. En pratique, les montures des pièces optiques, la taille d'un détecteur sont des diaphragmes. La suite précise cette notion.
Diaphragme de champ
Un diaphragme de champ limite la taille angulaire du faisceau. Il est dimensionné pour assurer :
- Un champ aux dimensions voulues.
- Une bonne qualité optique dans le champ.
- Un éclairement uniforme.
Le détecteur, de taille finie, peut jouer le rôle de diaphragme de champ.
Diaphragme d'ouverture
Dans un système optique centré, le diaphragme d'ouverture est le diaphragme matériel qui limite
l'ouverture d'un faisceau centré. C'est donc le diaphragme vu de puis l'objet sous le plus petit angle ; c'est souvent la monture de la première lentille.
Un diaphragme d'ouverture limite l'éclairement. Il est essentiellement dimensionné pour assurer le niveau d'éclairement voulu. Il joue sur l'extension linéaire du faisceau : un grand diaphragme nécessite des pièces optiques de grande taille... dont la qualité doit suivre.
Pupilles
La pupille d'entrée d'un instrument est l'image géométrique du diaphragme d'ouverture par les lentilles placées en avant ce diaphragme.
La pupille de sortie est l'image géométrique de la pupille d'entrée. C'est aussi l'image géométrique du diaphragme d'ouverture par les lentilles placées après ce diaphragme.
Diaphragme de champ
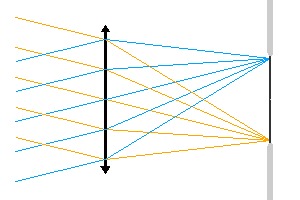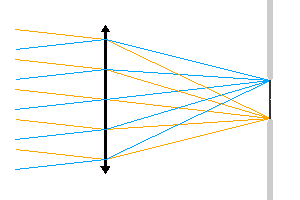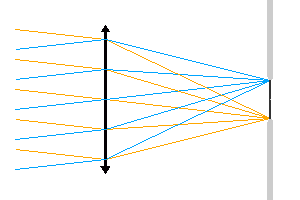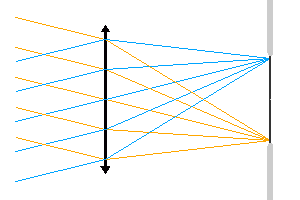
Relation entre la taille du détecteur, faisant office de diaphragme de champ, et le champ accessible.
Crédit :
ASM
Diaphragme de champ
Un diaphragme de champ limite l'ouverture angulaire du faisceau. Dans l'animation proposée, c'est la taille du détecteur qui limite le champ accessible : le détecteur joue le rôle de diaphragme de champ.
Diaphragme d'ouverture
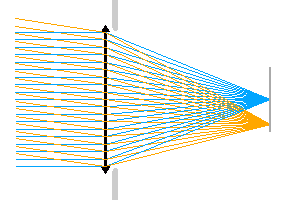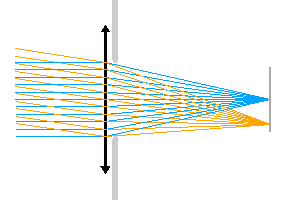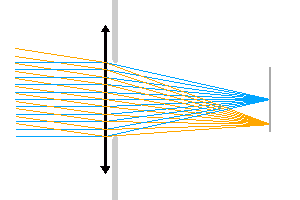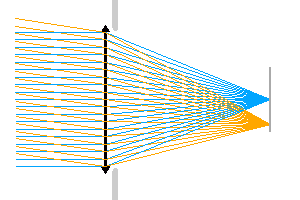
Relation entre le diaphragme d'ouverture et l'éclairement au foyer.
Crédit :
ASM
Diaphragme d'ouverture
Un diaphragme d'ouverture limite l'éclairement. Dans l'animation proposée, le diaphragme d'ouverture limite l'éclairement au foyer.
 Diaphragme d'ouverture
Diaphragme d'ouverture
Difficulté : ☆
Temps : 10 min
On propose d'utiliser un montage afocal, avec les lentilles L1 et L2 de caractéristiques respectives (focales et diamètres) :
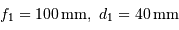 ;
;
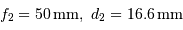 .
.
Question 1)
Sous quelle ouverture sont vues les lentilles depuis leur foyer commun ?
[1 points]
Question 2)
En déduire la lentille qui joue le rôle de diaphragme d'ouverture.
[1 points]
La question précédente suffit pour apporter la réponse.
 Pupille d'entrée de CoRoT
Pupille d'entrée de CoRoT
Difficulté : ☆☆
Temps : 30 min
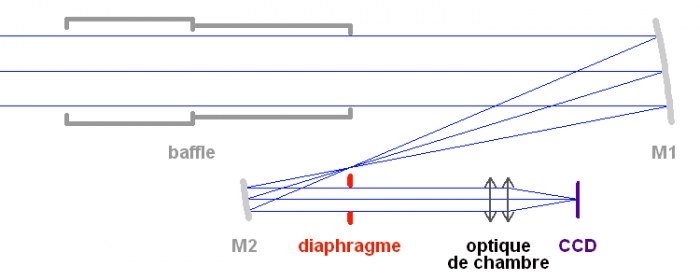
Schéma optique de CoRoT.
Crédit :
ASM
La figure représente le montage optique du collecteur du
satellite CoRoT. Il comporte un baffle de grande taille dont le
rôle est de protéger le signal de toute perturbation extérieure,
pour une étude photométrique extrêmement précise. Le montage
collecteur (miroirs M1 et M2) est hors-axe, afin d'éviter toutes
les réflexions parasites qu'apporterait le miroir secondaire M2
avec sa structure dans le cas d'un montage axial.
Question 1)
D'après le schéma optique, à quelle configuration correspond l'ensemble des miroirs collecteurs M1 et M2 ? Quelles sont les propriétés du faisceau après passage par M2, en terme de diamètre, ouverture et étendue de faisceau comparées aux mêmes valeurs en amont de M1 ?
[2 points]
Examiner le tracé de rayons.
Identitifier la nature des rayons incidents, émergents. Que se passe-t-il entre les miroirs M1 et M2?
Question 2)
Le diaphragme 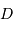 est positionné en aval de M2, à une distance du miroir égale à la focale de M2. En déduire la position de la pupille d'entrée
est positionné en aval de M2, à une distance du miroir égale à la focale de M2. En déduire la position de la pupille d'entrée 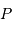 . Faire un schéma justifiant la réponse.
. Faire un schéma justifiant la réponse.
[2 points]
Le diaphragme 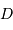 est un diaphragme d'ouverture.
est un diaphragme d'ouverture.
Se rappeler la définition de la pupille d'entrée, et le lien avec le diaphragme 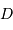 .
.
Question 3)
Que peut-on dire d'un photon qui passe par la pupille d'entrée ?
[1 points]
Quel lien encore entre diaphragme d'ouverture et diaphragme de champ ?
Question 4)
En fonction de ce qui précède, reformuler le rôle du baffle de protection.
[1 points]
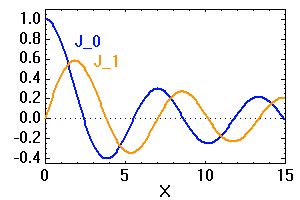
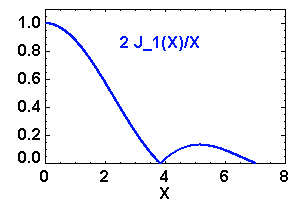
Les 2 premières fonctions de Bessel,
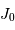
et
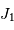
.
Crédit :
ASM
Fonctions de Bessel
La figure de diffraction d'une pupille circulaire introduit les fonctions de Bessel.
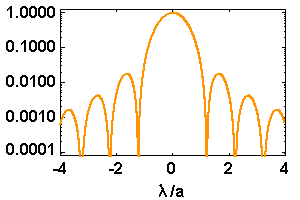
Coupe de la figure de diffraction, en représentation logarithmique et unité
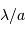
. Le premier zéro est à l'abscisse 1.22.
Crédit :
ASM
 Prérequis
Prérequis
Diffraction de Fraunhofer.
 Objectifs
Objectifs
(Page à n'aborder qu'en deuxième lecture).
Introduire, pour une pupille circulaire, les fonctions de Bessel, qui justifient le facteur 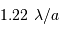 qui dimensionne la tache de diffraction.
qui dimensionne la tache de diffraction.
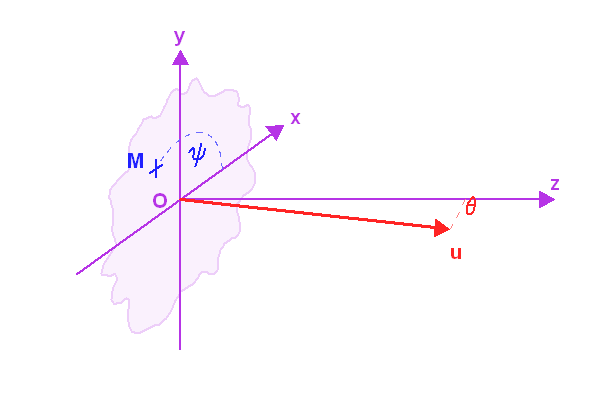
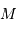
est un point courant de la pupille, de coordonnées polaires
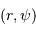
, et
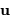
porte la direction pour laquelle on recherche l'amplitude de l'onde diffractée.
Crédit :
ASM
Pupille circulaire
La pupille étant circulaire, de rayon 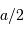 , il est préférable de décrire les coordonnées du point
, il est préférable de décrire les coordonnées du point 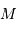 et de la direction de diffraction
et de la direction de diffraction 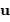 en coordonnées polaires, avec les notations suivantes :
en coordonnées polaires, avec les notations suivantes :
(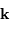 est le vecteur normal au plan de la pupille).
L'amplitude de l'onde diffractée dans la direction
est le vecteur normal au plan de la pupille).
L'amplitude de l'onde diffractée dans la direction 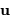 faisant un angle
faisant un angle 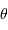 avec l'axe optique s'écrit alors, en supposant l'amplitude incidente uniforme :
avec l'axe optique s'écrit alors, en supposant l'amplitude incidente uniforme :
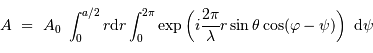
On introduit les fonctions de Bessel, dont les 2 premiers termes sont, par définition :
![\begin{eqnarray*} J_0 (X) =& \displaystyle{{1\over 2\pi} \int_0^{2\pi} \exp \bigl[-iX \cos v \bigr]\ {\mathrm{d}} v}\\ J_1 (X) =& \displaystyle{{1\over X}\ \int_0^{X} u J_0 (u)\ {\mathrm{d}} u}\\ \end{eqnarray*}](../pages_rayon/equations_diffraction-pupille/equation25.png)
L'amplitude diffractée dans une direction faisant un petit angle 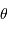 par rapport à l'axe optique, devient :
par rapport à l'axe optique, devient :
 Démonstration
Démonstration
Les calculs passent par les changements de variables
L'intensité diffractée dans la direction 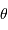 s'écrit donc :
s'écrit donc :
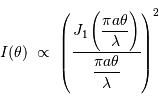
Zéros, anneaux et largeur à mi-hauteur
Pour 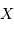 voisin de 0,
voisin de 0, 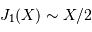 . Par ailleurs,
le premier zéro de la fonction
. Par ailleurs,
le premier zéro de la fonction 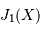 est pour
est pour 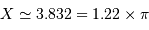 .
La largeur à mi-hauteur du pic central de diffraction, supposée égale à la demi-largeur entre les 2 zéros de part et d'autre du pic central, s'écrit en fonction du diamètre de la pupille
.
La largeur à mi-hauteur du pic central de diffraction, supposée égale à la demi-largeur entre les 2 zéros de part et d'autre du pic central, s'écrit en fonction du diamètre de la pupille 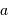 et de la longueur d'onde
et de la longueur d'onde 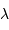 :
:
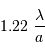
La figure de diffraction s'annule ensuite pour les rayons 2.23, 3.23, 4.24, 5.24.... en unité 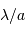 . Les anneaux lumineux ont comme rayon, dans la même unité : 1.63, 2.68, 3.70, 4.71, 5.71...
. Les anneaux lumineux ont comme rayon, dans la même unité : 1.63, 2.68, 3.70, 4.71, 5.71...

Pupille d'entrée et sa transformée de Fourier.
Crédit :
ASM
La TF de la pupille
La figure de diffraction d'une pupille, quelle qu'elle soit, est identique à sa
transformée de Fourier.
 Prérequis
Prérequis
Cours sur la diffraction de Fraunhofer.
 Objectifs
Objectifs
(Page à n'aborder qu'en 2eme lecture.)
Mettre en regard le formalisme décrivant la diffraction à l'infini par une pupille et le formalisme de la transformation de Fourier.
Diffraction et filtrage
On peut utiliser les propriétés de la TF pour réécrire les caractéristiques de la diffraction.
Une pupille de taille caractéristique 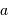 filtre les hautes fréquences, càd l'information angulaire plus fine typiquement que
filtre les hautes fréquences, càd l'information angulaire plus fine typiquement que 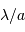 .
.
Plus la pupille est grande, moins elle filtre angulairement.
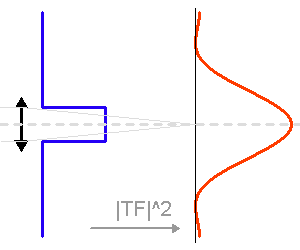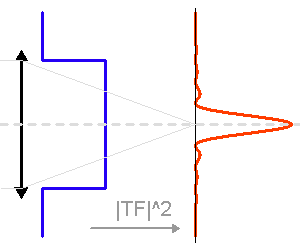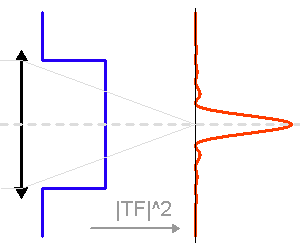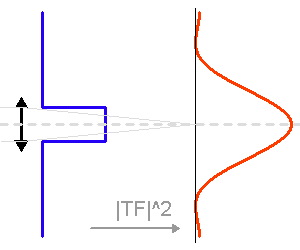
Pupille d'entrée et sa tache d'Airy : module carré de sa transformée de Fourier.
Crédit :
ASM
La TF de la pupille
La tache image due à la seule diffraction dépend du diamètre du télescope. Plus ce dernier est grand, plus la tache d'Airy est piquée.
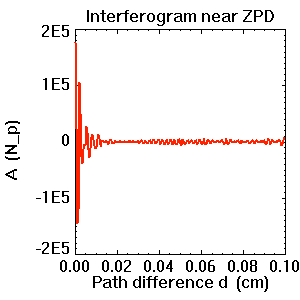
Portion de la partie modulée d'un interférogramme. Le contraste des franges s'écroule dès lors que l'on s'éloigne de la différence de marche nulle.
Crédit :
ASM
Interférogramme
Un interféromètre de Michelson permet de tracer l'interférogramme d'une source, càd la figure d'interférence obtenue après déphasage de l'une des 2 voies de l'interféromètre d'une différence de marche  .
L'interférogramme du
spectre d'une source réelle, délimitée par un intervalle spectral
fini, illustre le phénomène de cohérence temporelle : le signal
d'interférence chute dès lors que la différence de marche devient
grande.
.
L'interférogramme du
spectre d'une source réelle, délimitée par un intervalle spectral
fini, illustre le phénomène de cohérence temporelle : le signal
d'interférence chute dès lors que la différence de marche devient
grande.
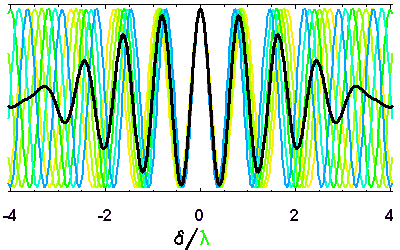
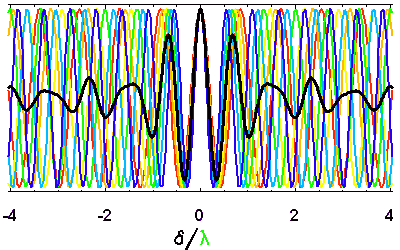
Evolution de la longueur de cohérence temporelle en fonction de la largeur spectrale. Plus l'intervalle spectral accepté est large, plus vite le signal est moyenné dès lors que la différence de marche s'éloigne de la valeur nulle.
Crédit :
ASM
Cohérence temporelle et intervalle spectral
La cohérence temporelle décroît d'autant plus rapidement que le spectre de la source présente une gamme de longueurs d'onde importante.
 Objectifs
Objectifs
Le cas d'une source rigoureusement ponctuelle et monochromatique est
souvent évoqué pour aborder l'optique géométrique et physique. Une source ne sera jamais totalement monochromatique,
même si son spectre présente des raies d'émission très étroites, ou si
par dispersion ou filtrage on sélectionne un très fin domaine
spectral. La cohérence temporelle d'une onde rend compte de sa chromaticité.
Une approche rigoureuse passe par le théorème de Wiener-Khintchine.
 Prérequis
Prérequis
Interféromètre de Michelson
Cohérence temporelle
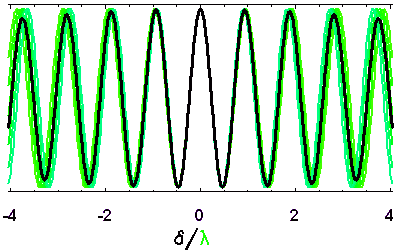
Tout phénomène d'interférence avec une source monochromatique conduit à une modulation de l'amplitude résultante fonction de la longueur d'onde du rayonnement.
Pour une source polychromatique, mélanger les couleurs revient donc à mélanger des périodes différentes : la cohérence temporelle du signal est prise en défaut.
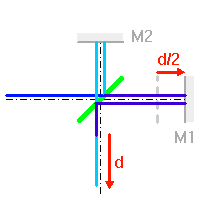
Interféromètre de Michelson : les 2 faisceaux, après recombinaison, sont décalés d'une différence de marche
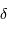
.
Crédit :
ASM
Exemple : interférométrie par transformée de Fourier
(Ne pas hésiter à aller voir les pages dédiées au spectromètre par TF).
L'exemple d'un interféromètre par transformée de Fourier (réglé en anneau) présente la problématique :
la visibilité des franges décroît d'autant plus rapidement que le
domaine spectral accepté est vaste.
Pour une raie monochromatique, l'interférogramme se développe, en fonction de la différence de marche, comme :
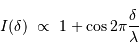
Pour une raie réelle, présentant une largeur non infiniment fine, il faut tenir compte de la contribution des différentes composantes spectrales.
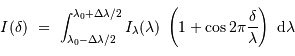
L'intégration, fonction du profil spectral 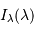 de la raie, conduit à :
de la raie, conduit à :
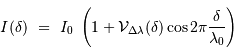
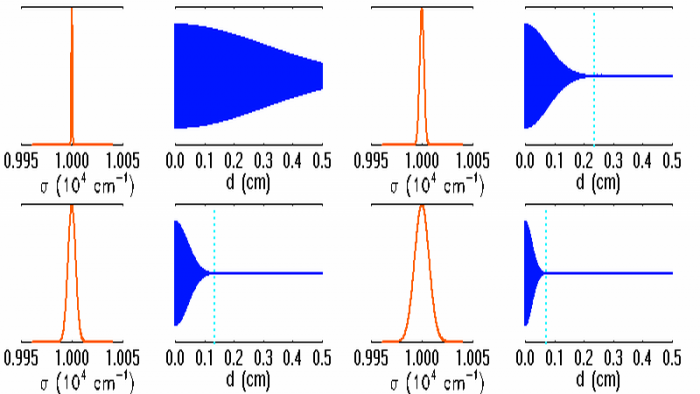
Profils de raie et visibilités associées.
Crédit :
ASM
L'expression de la fonction de visibilité des franges 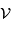 dépend de l'intégration du profil spectral
dépend de l'intégration du profil spectral 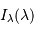 , et n'est pas nécessairement simple. La visibilité :
, et n'est pas nécessairement simple. La visibilité :
- a une extension inversement proportionnelle à
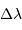 ; plus l'intervalle spectral est grand, moins les franges de l'interférogramme seront visibles.
; plus l'intervalle spectral est grand, moins les franges de l'interférogramme seront visibles. - décroît avec la différence de marche
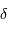 .
.
Un exemple de démonstration, dans un cas simplifié, est donné en exercice.
Définition de la cohérence temporelle
Dans le cas général, le degré de cohérence d'une source polychromatique, complexe, s'écrit :
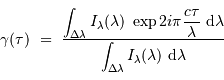
La démonstration résulte du théorème de Wiener-Khintchine.
La longueur de cohérence 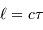 , qui mesure l'étendue du degré de cohérence, vérifie approximativement :
, qui mesure l'étendue du degré de cohérence, vérifie approximativement :
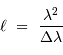
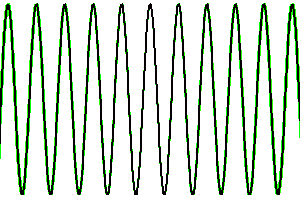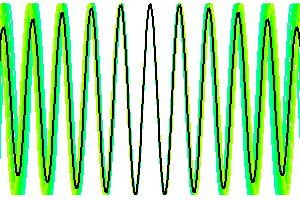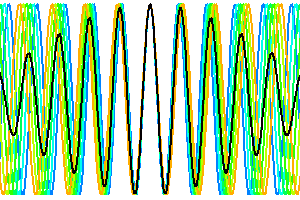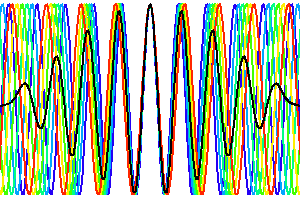
Evolution de la longueur de cohérence temporelle en fonction de la largeur spectrale.
Crédit :
ASM
Visibilité fonction de l'intervalle spectral
La visibilité des franges d'interférences dépend de la largeur de l'intervalle spectral considéré. La superposition de franges de couleurs différentes, donc de périodes différentes, conduit à un signal d'interférence en moyenne nulle.
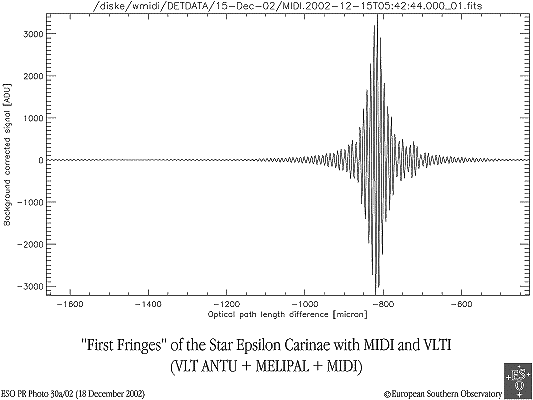
Enregistrement de franges d'interférence. La cohérence spatiale est limitée par la taille angulaire de la source.
Crédit :
ESO
Mesure de visibilité
Un interféromètre enregistre des franges d'interférence, pour en déterminer la visibilité. Celle-ci décroît rapidement dès que l'interférogramme s'écarte de la différence de marche correspondant au déphasage nul entre les 2 signaux.
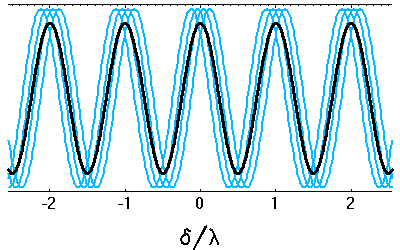
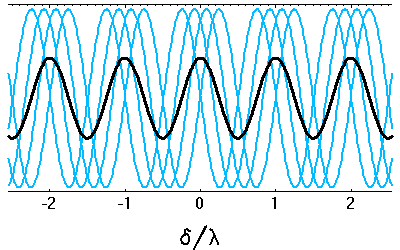
Cohérence spatiale : la superposition des différentes contributions déphasées amoindrit la visibilité des franges.
Crédit :
ASM
Source étendue
La cohérence spatiale entre 2 points d'un écran dépend de l'étendue angulaire de la source.

Tache de diffraction récupérée par optique adaptative (NACO/VLT) en bande K.
Crédit :
ESO
Source ponctuelle
L'image d'une source ponctuelle n'est pas un point : c'est la diffraction qui le veut... c'est un cas particulier de la notion de cohérence spatiale.
 Objectifs
Objectifs
Le cas d'une source rigoureusement ponctuelle et monochromatique est
souvent évoqué pour aborder l'optique (géométrique ou physique). Une source réelle en astrophysique peut être
approximativement ponctuelle, du fait d'un très grand éloignement, mais ce
n'est pas toujours le cas.
La cohérence spatiale rend compte de l'étendue angulaire de la source.
Une analyse détaillée des phénomènes peut se traiter par une formalisme
mathématique et s'appuie sur le théorème Zernike Van-Cittert.
Cohérence spatiale
Les sources astrophysiques ne sont pas naturellement cohérentes. Leur
étendue angulaire va conduire à dégrader la cohérence du rayonnement : l'onde collectée mélange diverses directions incidentes, présentant différentes phases, dont le mélange dégrade la cohérence.
Pour modéliser ce phénomène, on s'intéresse à la cohérence du champ sur un écran illuminé par une source à grande distance ; cet écran illustre le rôle que joue un plan d'onde intermédiaire ou bien une pupille.
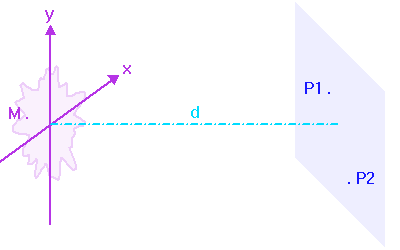
Cohérence du champ vu depuis 2 points P1 et P2 d'un écran E.
Crédit :
ASM
Cohérence du rayonnement d'une source circulaire.
Crédit :
ASM
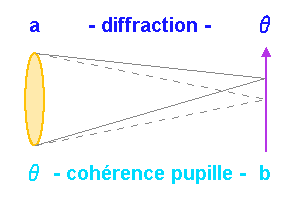
Ce schéma montre l'analogie entre le calcul de la tache de diffraction par une pupille circulaire de rayon
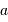
, et la cohérence du champ d'une source de diamètre
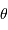
entre 2 points d'un écran séparés de
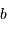
.
Crédit :
ASM
Rappel sur la diffraction de Fraunhofer
Le résultat précédent ressemble furieusement à celui de la diffraction. Est-ce un hasard ?
La tache d'Airy résultant de la diffraction par une pupille circulaire rend compte de la contribution de toutes les sources secondaires à considérer sur la pupille. Plus la pupille est grande, plus les déphasages s'accumulent dès lors que l'on s'éloigne de la position centrale de l'image géométrique. Il s'ensuit que la tache de diffraction est d'autant plus piquée que la pupille est grande.
En terme de cohérence, plus une pupille est grande, plus le degré de cohérence entre 2 points de cette pupille diminue.
Une autre manière de reformuler ceci dérive de l'analyse de Fourier :
plus on possède d'information sur un signal, moins ce signal est localisé.
Le principe d'incertitude de Heisenberg ne dit pas autre chose : la détermination précise d'une grandeur nécessite que sa grandeur conjuguée soit étendue, la moins localisée possible.
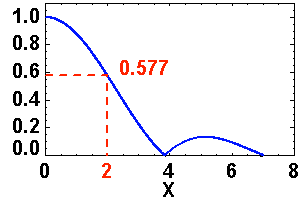
Etendue de cohérence : la valeur à mi-hauteur est obtenue pour
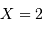
.
Crédit :
ASM
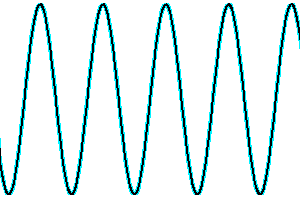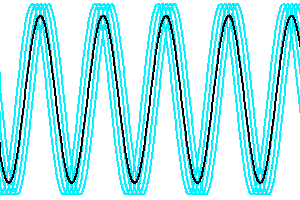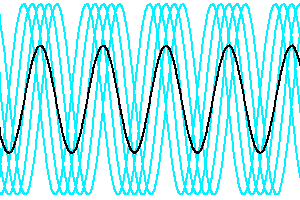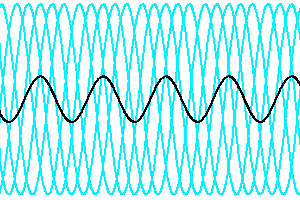
Evolution de la cohérence spatiale en fonction des déphasage des faisceaux issus de différents points de la source.
Crédit :
ASM
Visibilité fonction du degré de cohérence de la pupille
La visibilité du signal d'interférence dépend des déphasages entre les faisceaux issus des différents points de la source. Plus ces déphasages augmentent, moins le signal est cohérent.

Disque solaire, en lumière visible. Sa brillance n'est pas tout à fait uniforme : le phénomène d'assombrissement centre-bord rend compte des conditions différentes de transfert de rayonnement entre le centre et le limbe.
Crédit :
Observatoire de Paris
La mesure du diamètre angulaire de l'étoile
du Bouvier (Arcturus) résulte de la visibilité des franges d'interférence obtenues par interférométrie.
Crédit :
Observatoire de Paris
Diamètre stellaire
L'immense majorité des disques stellaires ne peut pas être résolue par imagerie avec un seul collecteur. Il est nécessaire, pour pallier cet effet, de recourir à la technique d'interférométrie.
La visibilité des franges d'interférence d'une source stellaire conduit alors de à la mesure de son diamètre.
 Objectifs
Objectifs
Nombre de sources astrophysiques présentent un diamètre angulaire qui ne peut pas être résolu par une pupille unique. Mais l'interférométrie permet d'affiner la résolution angulaire, et de mesurer des diamètres stellaires.
Source ponctuelle étendue
Le diamètre d'une étoile du proche environnement solaire sous-tend un
angle de l'ordre d'une milliseconde d'arc. Ce diamètre est, sauf exception,
très inférieur à la largeur de la tache de diffraction dans le visible d'un télescope, même de grand diamètre. En revanche, par interférométrie, on peut avoir accès indirectement à ce diamètre, si l'on dispose d'une base suffisamment grande.
On suppose une source de brillance uniforme, circulaire de diamètre angulaire
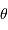 , observée par 2 télescopes identiques séparés d'une base
, observée par 2 télescopes identiques séparés d'une base
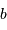 (base projetée dans le plan perpendiculaire à la source) que l'on fait interférer.
(base projetée dans le plan perpendiculaire à la source) que l'on fait interférer.
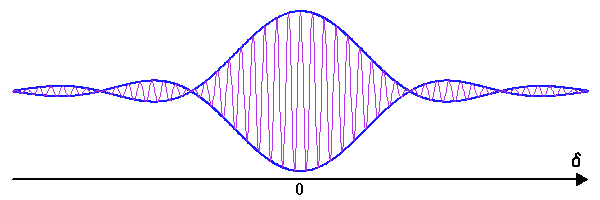
Franges d'interférence (en violet) et fonction de visibilité (courbe rouge).
Crédit :
ASM
Visibilité et mesure du diamètre stellaire
Le facteur de cohérence
établi dans le cas général est usuellement dénommé visibilité. La fonction de visibilité s'écrit :
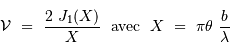
où 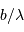 est la fréquence spatiale.
est la fréquence spatiale.
Chaque base 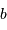 conduit à une mesure de la visibilité pour la fréquence spatiale
conduit à une mesure de la visibilité pour la fréquence spatiale 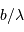 . Dans le cadre du modèle, où une étoile est un disque de brillance uniforme, la visibilité s'annule pour
. Dans le cadre du modèle, où une étoile est un disque de brillance uniforme, la visibilité s'annule pour 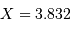 , et donc pour une relation entre le diamètre angulaire stellaire et la fréquence spatiale telle que :
, et donc pour une relation entre le diamètre angulaire stellaire et la fréquence spatiale telle que :
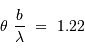
Finalement, une mesure du diamètre stellaire  revient à une mesure de visibilité de la figure d'interférence.
revient à une mesure de visibilité de la figure d'interférence.
Le calcul précédent a supposé que la source présente un profil de brillance uniforme : en fait le phénomène d'assombrissement centre-bord complique un peu l'analyse.
Le rôle de la diffraction ne peut bien sûr pas être négligé : toute mesure de visibilité doit être corrigée de la fonction d'appareil des collecteurs (dont la diffraction), que l'on détermine expérimentale sur une source vraiment ponctuelle (en pratique : très lointaine).
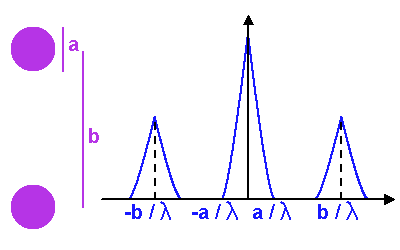
Diagramme donnant intensité en fonction de la fréquence spatiale, pour un interféromètre à 2 télescopes, de diamètre
, sur une base
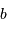
. L'autocorrélation de la pupille donne accès aux hautes fréquences spatiales
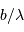
.
Crédit :
ASM
Résolution angulaire
Une pupille unique est un filtre passe-bas, coupant à la fréquence spatiale 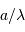 , et donnant une résolution angulaire de
, et donnant une résolution angulaire de 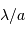 .
.
Un interféromètre est donc un filtre passe-bande, qui fournit une information à la fréquence 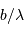 ; sa résolution angulaire est
; sa résolution angulaire est 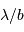 .
.
On retrouve ces propriétés par une analyse en terme de Fourier : le théorème de Wiener-Khintchine relie la fonction de transfert optique à la TF inverse de l'autocorrélation de la pupille.
Synthèse d'ouverture
Une mesure du facteur de cohérence complexe fournit une composante de fréquence spatiale de la source. La mesure de ce facteur à plusieurs fréquences spatiales permet la reconstruction de la distribution spatiale d'intensité de la source.
 QCM
QCM
 Diamètre stellaire
Diamètre stellaire
Difficulté : ☆☆
Temps : 20 min
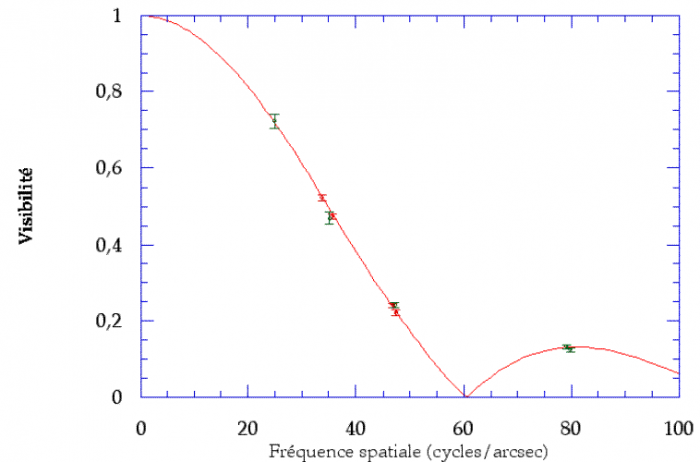
Les figures ci-jointes illustrent la mesure de visibilité de franges d'interférence.
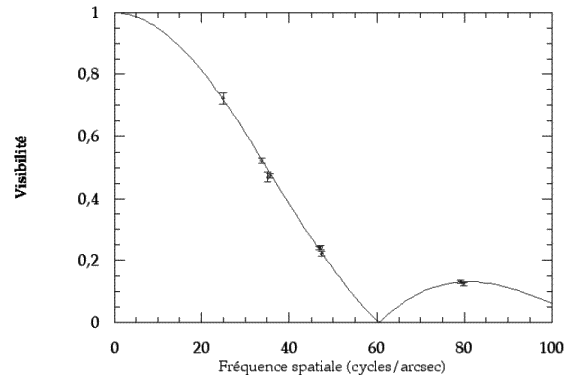
Courbe de visibilité de l'étoile
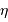
du Bouvier.
Crédit :
Observatoire de Paris
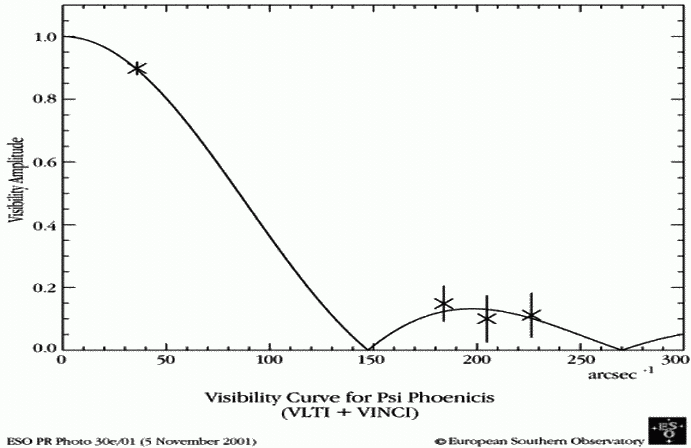
Courbe de visibilité de l'étoile
de la constellation du Phénix.
Crédit :
ESO
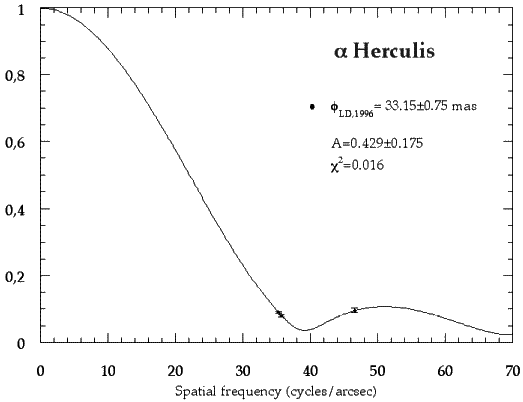
Courbe de visibilité de l'étoile
de la constellation d'Hercule.
Crédit :
ESO
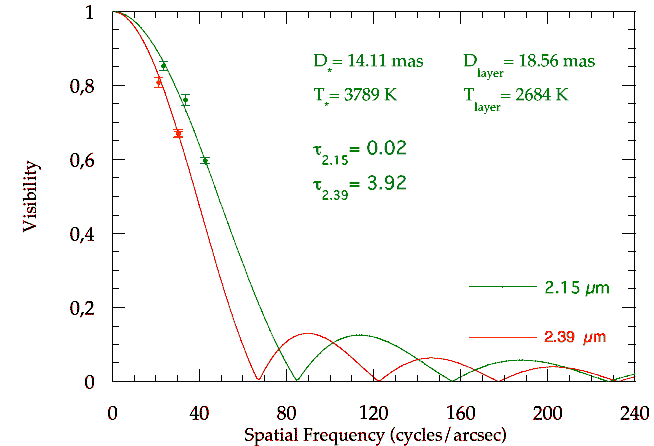
Courbes de visibilité de l'étoile
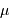
de Céphée.
Crédit :
Observatoire de Paris
Question 1)
Déduire des courbes le diamètre angulaire des sources stellaires 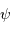 Phe et
Phe et 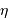 Boo.
Boo.
Rechercher le premier minimum de la fonction de visibilité.
Question 2)
Quelle raison physique peut expliquer que la courbe de visibilité de
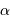 d'Hercule ne s'annule pas.
d'Hercule ne s'annule pas.
Quelle hypothèse sous-tend le résultat ?
Question 4)
Discuter les courbes de la figure concernant l'étoile 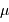 Cep.
Cep.
Est-ce normal d'avoir 2 courbes de visibilité différentes à 2 longueurs d'onde différentes ?
Que signifie la détermination de 2 diamètres stellaires différents pour 2 longueurs d'onde différentes ?
- Question 1
Aide :
Se servir la conservation de l'étendue de faisceau
Solution :
Si l'optique est bien conçue (sans diaphragme gênant), l'étendue
de faisceau se conserve. La traduction de 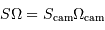 donne un angle solide objet
donne un angle solide objet
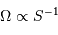
. Plus la
surface du collecteur est grande, plus le champ objet est réduit.
- Question 2
Aide :
Comment varie le nombre de photons collectés avec la surface collectrice ?
Solution :
Le nombre de photons collectés varie linéairement avec la surface collectrice. Le temps de pose varie donc en raison inverse :
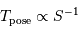
.
Plus la surface du collecteur est grande, plus le temps de pose est réduit.
- Question 3
Aide :
Se servir des 2 questions précédentes.
Aide :
Comparer la dépendance vis à vis de la surface collectrice 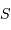 de la taille du champ élémentaire et du temps de pose élémentaire.
de la taille du champ élémentaire et du temps de pose élémentaire.
Solution :
La taille angulaire du champ élémentaire accessible varie comme 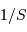 , la surface collectrice. Le temps de pose élémentaire varie comme
, la surface collectrice. Le temps de pose élémentaire varie comme 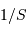 . Pour couvrir un champ donné, la durée totale ne dépend donc pas de la taille du télescope : le champ couvert en 1 pose de durée
. Pour couvrir un champ donné, la durée totale ne dépend donc pas de la taille du télescope : le champ couvert en 1 pose de durée 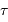 avec un petit collecteur sera observée par
avec un petit collecteur sera observée par 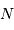 poses de durées
poses de durées 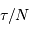 avec un grand.
avec un grand.
Notons que le télescope CFH, ouvert en 1980 avec un diamètre du collecteur de 3.6 m, s'est converti à partir des années 2000 vers l'imagerie grand champ.
- Question 1
Aide :
Revoir la page sur le montage afocal.
Solution :
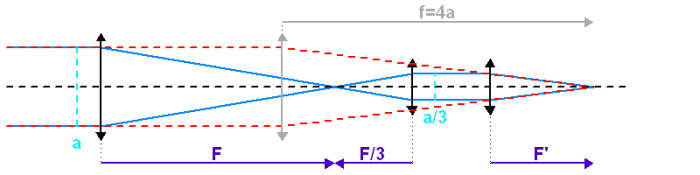
Le schéma équivalent correspond à un montage afocal suivi de l'optique de chambre
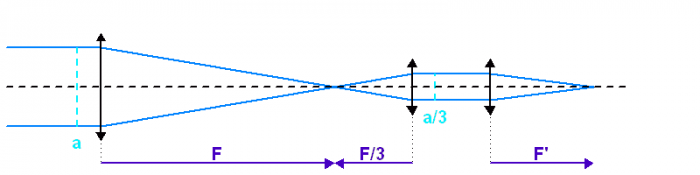
Ce montage afocal tient ici déjà compte de la suite, concernant le dimensionnement du miroir secondaire.
Crédit :
ASM
Remarque : pourquoi l'emploi des deux adjectifs, afocal et confocal, pour un même concept ? En fait, tout dépend du point de vue : si l'on s'intéresse aux dioptres, ils partagent un même foyer, d'où la dénomination confocale. Mais si l'on s'intéresse au faisceau, il passe de l'infini à l'infini, d'où la dénomination afocale.
- Question 2
Aide :
Revoir (encore !) la page sur le montage afocal.
Solution :
Par application directe des propriétés du montage afocal, le diamètre de la 2ème parabole comme celui des lentilles vaut le tiers de celui du primaire, soit 10 cm. Ce montage permet de réduire la taille des 6 lentilles de l'optique de chambre (intéressant en terme de poids et de coût). Mais, par conservation de l'étendue de faisceau, ces optiques travaillent sur des rayons d'inclinaison triplée.
- Question 3
Solution :
Le schéma équivalent demande 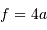 . L'étendue du faisceau s'écrit dont de 2 façons différentes, selon que l'on considère le montage réel ou le montage équivalent :
. L'étendue du faisceau s'écrit dont de 2 façons différentes, selon que l'on considère le montage réel ou le montage équivalent :
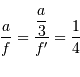
L'application numérique donne : 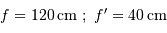
Le schéma équivalent demande
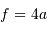
.
Crédit :
ASM
- Question 4
Aide :
Simple application de la conservation de l'étendue de faisceau.
Solution :
Par conservation de l'étendue de faisceau, la diminution du diamètre du faisceau par un facteur 3 s'accompagne par un accroissement dans un même facteur de l'ouverture.
Ainsi, le gain en taille doit être compensée par une meilleure qualité optique de ces lentilles travaillant avec rayons plus inclinés sur l'axe optique.
- Question 1
Aide :
Rechercher le premier minimum de la fonction de visibilité.
Solution :
Les diamètres stellaires sont respectivement :
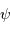 Phe : 1/147 = 6.8 mas
Phe : 1/147 = 6.8 mas
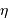 Boo : 1/61 = 16.4 mas
Boo : 1/61 = 16.4 mas
- Question 2
Aide :
Quelle hypothèse sous-tend le résultat ?
Solution :
Un profil de type d'Airy suppose que le disque stellaire présente une brillance uniforme.
Ici, ce n'est visiblement pas le cas.
- Question 3
Aide :
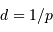 donne directement la distance en parsec si la parallaxe
donne directement la distance en parsec si la parallaxe 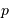 est mesurée en seconde d'arc.
est mesurée en seconde d'arc.
Solution :
Les distances de ces étoiles, sont alors, en parsec puis en unité métrique :
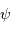 Phe : 99 pc,
Phe : 99 pc, 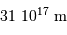 .
.
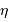 Boo : 11 pc, 3.5 ...
Boo : 11 pc, 3.5 ...
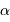 Her : 118 pc, 36 ...
Her : 118 pc, 36 ...
On en déduit ensuite les diamètres, en unité 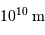 , puis en diamètre solaire et unité astronomique :
, puis en diamètre solaire et unité astronomique :
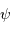 Phe : 10.4, soit 74 fois le diamètre solaire, ou 0.70 UA.
Phe : 10.4, soit 74 fois le diamètre solaire, ou 0.70 UA.
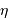 Boo : 2.9, ... 20.5 ... 0.19
Boo : 2.9, ... 20.5 ... 0.19
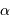 Her : 42, ... 300 ... 2.8
Her : 42, ... 300 ... 2.8
Il s'agit là d'étoiles géantes ou supergéantes, et non de naines.
- Question 4
Aide :
Est-ce normal d'avoir 2 courbes de visibilité différentes à 2 longueurs d'onde différentes ?
Aide :
Que signifie la détermination de 2 diamètres stellaires différents pour 2 longueurs d'onde différentes ?
Solution :
La visibilité dépend a priori de la longueur d'onde d'observation. Mais, dans la cas représenté, l'abscisse du graphe étant la fréquence spatiale, plus aucun paramètre ne dépend de la longueur d'onde. On en déduit que le diamètre stellaire sondé varie avec la longueur d'onde.
Pour cette étoile, la photosphère, de diamètre de l'ordre de 14 mas, est entourée d'une couche de diamètre 18.6 mas transparente à 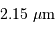 mais opaque à
mais opaque à 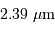 .
.








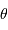 entre un point de l'objet et le point de l'objet centré sur l'axe optique ; la distance
entre un point de l'objet et le point de l'objet centré sur l'axe optique ; la distance 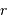 , sur la
, sur la 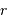 . Elle est d'autant plus grande que l'ouverture de l'optique est grande.
. Elle est d'autant plus grande que l'ouverture de l'optique est grande.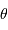 , indépendamment de la taille de l'optique. La
, indépendamment de la taille de l'optique. La 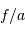 et de la distance angulaire
et de la distance angulaire 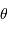 .
.


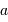 en un faisceau de diamètre
en un faisceau de diamètre 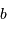 , avec un grossissement angulaire
, avec un grossissement angulaire 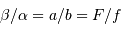 .
.
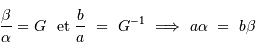

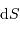 à l'aire collectrice
à l'aire collectrice 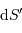 .
.
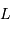 transportée par un faisceau lumineux, émise par l'élément de surface S et reçue par S' se conserve (sorte de tautologie, le faisceau étant défini par l'ensemble des rayons lumineux, càd la totalité de la puissance lumineuse). Cette puissance est proportionnelle à la
transportée par un faisceau lumineux, émise par l'élément de surface S et reçue par S' se conserve (sorte de tautologie, le faisceau étant défini par l'ensemble des rayons lumineux, càd la totalité de la puissance lumineuse). Cette puissance est proportionnelle à la 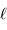 , à l'élément de surface émetteur et à l'élément d'angle solide d'émission.
, à l'élément de surface émetteur et à l'élément d'angle solide d'émission.
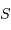 , occupant un angle solide
, occupant un angle solide 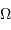 , dans un milieu d'indice unité (comme le vide ou comme l'air à peu de chose près), par le produit
, dans un milieu d'indice unité (comme le vide ou comme l'air à peu de chose près), par le produit 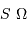 , qui se conserve le long du faisceau.
, qui se conserve le long du faisceau.
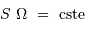
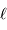 à la puissance lumineuse nécessite de s'appuyer sur le produit d'un élément de surface émetteur
à la puissance lumineuse nécessite de s'appuyer sur le produit d'un élément de surface émetteur 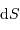 et d'un angle solide d'émission
et d'un angle solide d'émission 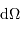 .
La luminosité élémentaire s'écrit :
.
La luminosité élémentaire s'écrit :
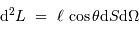
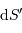 à la distance
à la distance 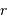 telle que :
telle que :
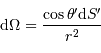
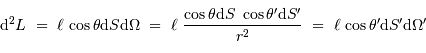
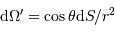 l'angle solide sous lequel est vue la source depuis la surface réceptrice. On remarque que le rôle des éléments émetteur et récepteur est symétrique. Le produit
l'angle solide sous lequel est vue la source depuis la surface réceptrice. On remarque que le rôle des éléments émetteur et récepteur est symétrique. Le produit 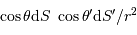 introduit l'étendue géométrique élémentaire.
introduit l'étendue géométrique élémentaire.
 angle solide
angle solide 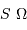 .
.

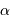 couvre un angle solide :
couvre un angle solide :
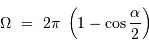
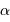 est petit, cet angle solide se réécrit simplement :
est petit, cet angle solide se réécrit simplement :
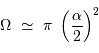
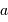 , la conservation du produit
, la conservation du produit 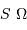 devient, pour ce faisceau conique :
devient, pour ce faisceau conique :
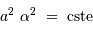
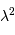 .
La justification est donnée en
.
La justification est donnée en 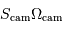 . Le but de l'exercice est de déterminer quel collecteur optimal utiliser pour réaliser ce programme.
. Le but de l'exercice est de déterminer quel collecteur optimal utiliser pour réaliser ce programme.
 du collecteur ?
du collecteur ?
 de la taille du champ élémentaire et du temps de pose élémentaire.
de la taille du champ élémentaire et du temps de pose élémentaire.

 même foyer) hors axe, suivis par une optique de chambre conjuguant le faisceau issu des 2 paraboles avec le détecteur CCD. En pratique, pour les respecter les specifications de la formation d'image, cette optique de chambre est constituée de 6 lentilles.
même foyer) hors axe, suivis par une optique de chambre conjuguant le faisceau issu des 2 paraboles avec le détecteur CCD. En pratique, pour les respecter les specifications de la formation d'image, cette optique de chambre est constituée de 6 lentilles.
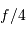 vu par la caméra, Calculer la focale
vu par la caméra, Calculer la focale 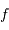 équivalente et la focale
équivalente et la focale 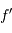 de l'optique de chambre.
de l'optique de chambre.
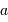 délivre une tache de diffraction d'ouverture (définie comme largeur à mi-hauteur)
délivre une tache de diffraction d'ouverture (définie comme largeur à mi-hauteur) 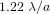 . On cherche à en déduire l'étendue de faisceau cohérente.
. On cherche à en déduire l'étendue de faisceau cohérente.
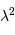 .
.
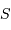 et
et 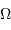 .
.
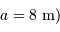 est alimenté par un faisceau de fibres de diamètre
est alimenté par un faisceau de fibres de diamètre 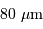 .
.
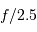 . En déduire l'ouverture angulaire du faisceau en entrée de fibre.
. En déduire l'ouverture angulaire du faisceau en entrée de fibre.
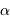 par un collecteur de diamètre
par un collecteur de diamètre 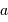 et de focale
et de focale 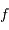 . On considère le seul cas où l'angle
. On considère le seul cas où l'angle 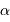 est petit. On note
est petit. On note 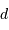 ladite taille linéaire.
ladite taille linéaire.
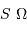 côté source, en fonction des données.
côté source, en fonction des données.
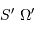 côté détecteur.
côté détecteur.
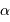 , quelle est la taille linéaire
, quelle est la taille linéaire 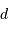 de son image.
de son image.




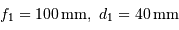 ;
;
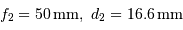 .
.

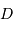 est positionné en aval de M2, à une distance du miroir égale à la focale de M2. En déduire la position de la pupille d'entrée
est positionné en aval de M2, à une distance du miroir égale à la focale de M2. En déduire la position de la pupille d'entrée 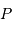 . Faire un schéma justifiant la réponse.
. Faire un schéma justifiant la réponse.
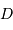 est un diaphragme d'ouverture.
est un diaphragme d'ouverture.
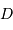 .
.

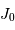 et
et 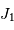 .
.

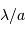 . Le premier zéro est à l'abscisse 1.22.
. Le premier zéro est à l'abscisse 1.22.
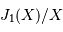 , avec
, avec 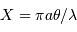 , avec
, avec 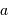 le diamètre de la pupille,
le diamètre de la pupille, 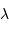 la longueur d'onde et
la longueur d'onde et 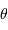 la direction d'observation.
la direction d'observation.
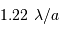 qui dimensionne la tache de diffraction.
qui dimensionne la tache de diffraction.
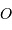 , et l'on note
, et l'on note 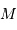 un point de la pupille. Cette pupille est éclairée par une onde plane uniforme, monochromatique, en incidence normale. L'amplitude de l'onde diffractée dans une direction repérée par le vecteur directeur
un point de la pupille. Cette pupille est éclairée par une onde plane uniforme, monochromatique, en incidence normale. L'amplitude de l'onde diffractée dans une direction repérée par le vecteur directeur 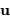 s'écrit :
s'écrit :
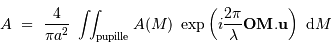

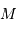 est un point courant de la pupille, de coordonnées polaires
est un point courant de la pupille, de coordonnées polaires 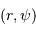 , et
, et 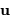 porte la direction pour laquelle on recherche l'amplitude de l'onde diffractée.
porte la direction pour laquelle on recherche l'amplitude de l'onde diffractée.
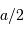 , il est préférable de décrire les coordonnées du point
, il est préférable de décrire les coordonnées du point 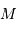 et de la direction de diffraction
et de la direction de diffraction 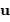 en coordonnées polaires, avec les notations suivantes :
en coordonnées polaires, avec les notations suivantes :
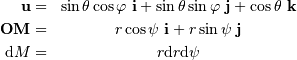
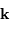 est le vecteur normal au plan de la pupille).
L'amplitude de l'onde diffractée dans la direction
est le vecteur normal au plan de la pupille).
L'amplitude de l'onde diffractée dans la direction 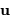 faisant un angle
faisant un angle 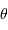 avec l'axe optique s'écrit alors, en supposant l'amplitude incidente uniforme :
avec l'axe optique s'écrit alors, en supposant l'amplitude incidente uniforme :
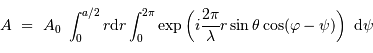
![\begin{eqnarray*} J_0 (X) =& \displaystyle{{1\over 2\pi} \int_0^{2\pi} \exp \bigl[-iX \cos v \bigr]\ {\mathrm{d}} v}\\ J_1 (X) =& \displaystyle{{1\over X}\ \int_0^{X} u J_0 (u)\ {\mathrm{d}} u}\\ \end{eqnarray*}](../pages_rayon/equations_diffraction-pupille/equation25.png)
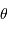 par rapport à l'axe optique, devient :
par rapport à l'axe optique, devient :
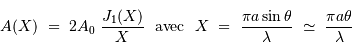
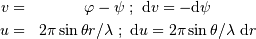
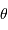 s'écrit donc :
s'écrit donc :
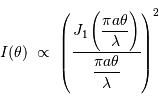
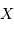 voisin de 0,
voisin de 0, 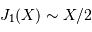 . Par ailleurs,
le premier zéro de la fonction
. Par ailleurs,
le premier zéro de la fonction 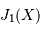 est pour
est pour 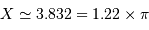 .
La largeur à mi-hauteur du pic central de diffraction, supposée égale à la demi-largeur entre les 2 zéros de part et d'autre du pic central, s'écrit en fonction du diamètre de la pupille
.
La largeur à mi-hauteur du pic central de diffraction, supposée égale à la demi-largeur entre les 2 zéros de part et d'autre du pic central, s'écrit en fonction du diamètre de la pupille 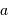 et de la longueur d'onde
et de la longueur d'onde 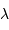 :
:
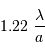
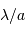 . Les anneaux lumineux ont comme rayon, dans la même unité : 1.63, 2.68, 3.70, 4.71, 5.71...
. Les anneaux lumineux ont comme rayon, dans la même unité : 1.63, 2.68, 3.70, 4.71, 5.71...

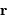 , la fonction
, la fonction 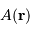 caractérisant l'éclairement sur la pupille, l'amplitude diffractée
dans une direction angulaire de vecteur directeur
caractérisant l'éclairement sur la pupille, l'amplitude diffractée
dans une direction angulaire de vecteur directeur 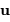 s'écrit :
s'écrit :
![\begin{eqnarray*} A ( \mathbf{u})\ &=&\ \int\!\!\!\int_{\mathrm{ pupille }} A( \mathbf{r} ) \exp\left[ -2i\pi \mathbf{u}. { \mathbf{r} \over \lambda} \right] \ \ { {\mathrm{d}} \mathbf{r}\over \lambda^2}\\ &=& \ \int\!\!\!\int {\cal P}( \mathbf{r})\ I( \mathbf{r} ) \exp\left[ -2i\pi \mathbf{u}. { \mathbf{r} \over \lambda} \right]\ \ { {\mathrm{d}} \mathbf{r}\over \lambda^2}\\ \end{eqnarray*}](../pages_rayon/equations_diffraction-fourier/equation4.png)
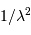 introduit pour normaliser l'élément de surface
introduit pour normaliser l'élément de surface 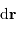 , et
, et
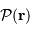 la pupille d'entrée, qui limite la fraction de l'onde plane
émise par la source à l'infini. Pour un éclairement uniforme en incidence normale,
la pupille d'entrée, qui limite la fraction de l'onde plane
émise par la source à l'infini. Pour un éclairement uniforme en incidence normale, 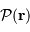 est typiquement une fonction porte à 2 dimensions.
est typiquement une fonction porte à 2 dimensions.
![\tilde f ( \mathbf{u}) \ =\ \int\!\!\!\int f( \mathbf{r} ) \exp\left[ -2i\pi \mathbf{u} . \mathbf{r} \right] \ \ {\mathrm{d}} \mathbf{r}](../pages_rayon/equations_diffraction-fourier/equation9.png)
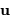 est donnée par la transformée de Fourier de la fonction
de pupille
est donnée par la transformée de Fourier de la fonction
de pupille 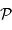 , la variable de position étant normalisée en unité de longueur d'onde :
, la variable de position étant normalisée en unité de longueur d'onde :
![A ( \mathbf{u})\ =\ A_0 \ \int\!\!\!\int {\cal P}( \mathbf{r})\ \exp\left[ -2i\pi \mathbf{u}. { \mathbf{r} \over \lambda} \right]\ \ { {\mathrm{d}} \mathbf{r}\over \lambda^2}](../pages_rayon/equations_diffraction-fourier/equation12.png)
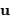 , et
, et 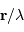 la variable spatiale décrivant la pupille rapportée à la longueur d'onde.
la variable spatiale décrivant la pupille rapportée à la longueur d'onde.
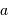 filtre les hautes fréquences, càd l'information angulaire plus fine typiquement que
filtre les hautes fréquences, càd l'information angulaire plus fine typiquement que 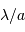 .
.


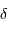 .
L'
.
L'



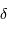 .
.
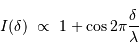
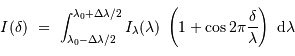
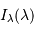 de la raie, conduit à :
de la raie, conduit à :
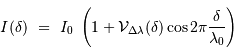

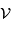 dépend de l'intégration du profil spectral
dépend de l'intégration du profil spectral 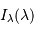 , et n'est pas nécessairement simple. La visibilité :
, et n'est pas nécessairement simple. La visibilité :
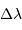 ; plus l'intervalle spectral est grand, moins les franges de l'interférogramme seront visibles.
; plus l'intervalle spectral est grand, moins les franges de l'interférogramme seront visibles.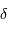 .
.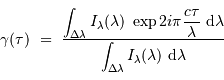
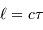 , qui mesure l'étendue du degré de cohérence, vérifie approximativement :
, qui mesure l'étendue du degré de cohérence, vérifie approximativement :
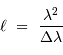






 de la source par le rayon vecteur
de la source par le rayon vecteur  de coordonnées
de coordonnées 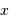 et
et 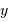 . On compare la cohérence entre 2 points
. On compare la cohérence entre 2 points 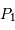 et
et 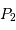 de l'écran.
Pour une source à grande distance (
de l'écran.
Pour une source à grande distance (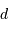 très grand par rapport aux autres dimensions), on définit le degré de cohérence comme une fonction du profil de brillance
très grand par rapport aux autres dimensions), on définit le degré de cohérence comme une fonction du profil de brillance 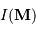 :
:
![\gamma_{1,2} \ = \ \gamma (\mathbf{P_1P_2}) \ = \ { \displaystyle{\int _{\mathrm{source}} I( \mathbf{M})\ \exp \left[ -2i\pi\ { \mathbf{M} \over d}. {\mathbf{P_1P_2} \over \lambda} \right] \ {\mathrm{d}}^2 \mathbf{M}} \over \displaystyle{\int _{\mathrm{source}} I( \mathbf{M}) \ {\mathrm{d}}^2 \mathbf{M}} }](../pages_rayon/equations_coherence-spatiale/equation9.png)

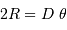 ,
de brillance uniforme, observée à distance
,
de brillance uniforme, observée à distance 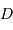 . La brillance peut être représentée par une fonction porte
. La brillance peut être représentée par une fonction porte 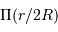 . On traite alors ce cas particulier en s'appuyant sur sa géométrie cylindrique, et
l'on réécrit la cohérence entre le centre
. On traite alors ce cas particulier en s'appuyant sur sa géométrie cylindrique, et
l'on réécrit la cohérence entre le centre 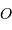 de l'écran (centre repéré sur la normale à l'écran vers la source) et un point
de l'écran (centre repéré sur la normale à l'écran vers la source) et un point 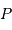 tel
tel 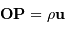 :
:
![\begin{eqnarray*} \gamma_{1,2} \ =& { \displaystyle{\int _{\mathrm{source}} \ \Pi{\left({D \mathbf{u}\over 2R } \right)}\exp\left[ -2i\pi\ \mathbf{u} . {\mathbf{\rho} \over \lambda}\right] \ {\mathrm{d}} \mathbf{u}} \over \displaystyle{\int _{\mathrm{source}} \Pi{\left({D \mathbf{u}\over 2R } \right)}\ {\mathrm{d}} \mathbf{u}} }\\ \propto & \displaystyle{\int_0^\theta \ \exp\left[ -2i\pi\ \mathbf{u} . {\mathbf{\rho} \over \lambda}\right] \ {\mathrm{d}} \mathbf{u}} \ = \ \displaystyle{ 2 J_1 \left( 2\pi\theta \displaystyle{\rho\over \lambda}\right) \over 2\pi\theta \displaystyle{\rho\over \lambda}}\\ = & \displaystyle{ 2 J_1 (X) \over X} \ \ \mathrm{avec} \ \ X\ =\ 2\pi\theta \displaystyle{\rho\over \lambda} \end{eqnarray*}](../pages_rayon/equations_coherence-spatiale/equation16.png)
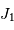 .
.

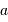 , et la cohérence du champ d'une source de diamètre
, et la cohérence du champ d'une source de diamètre 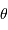 entre 2 points d'un écran séparés de
entre 2 points d'un écran séparés de 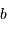 .
.

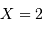 .
.
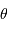 est vue depuis l'écran sous un angle solide
est vue depuis l'écran sous un angle solide 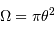 . Une surface
. Une surface 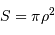 de l'écran correspond à une
de l'écran correspond à une 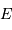 telle que :
telle que :
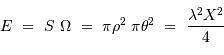
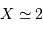 : on choisit cette valeur pour définir le rayon de l'étendue de cohérence.
: on choisit cette valeur pour définir le rayon de l'étendue de cohérence.
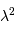 .
.



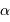 du Bouvier (Arcturus) résulte de la visibilité des franges d'interférence obtenues par interférométrie.
du Bouvier (Arcturus) résulte de la visibilité des franges d'interférence obtenues par interférométrie.
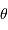 , observée par 2 télescopes identiques séparés d'une base
, observée par 2 télescopes identiques séparés d'une base
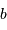 (base projetée dans le plan perpendiculaire à la source) que l'on fait interférer.
(base projetée dans le plan perpendiculaire à la source) que l'on fait interférer.

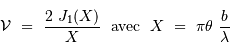
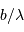 est la fréquence spatiale.
est la fréquence spatiale.
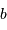 conduit à une mesure de la
conduit à une mesure de la 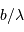 . Dans le cadre du modèle, où une étoile est un disque de brillance uniforme, la visibilité s'annule pour
. Dans le cadre du modèle, où une étoile est un disque de brillance uniforme, la visibilité s'annule pour 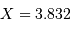 , et donc pour une relation entre le diamètre angulaire stellaire et la fréquence spatiale telle que :
, et donc pour une relation entre le diamètre angulaire stellaire et la fréquence spatiale telle que :
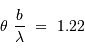
 revient à une mesure de visibilité de la figure d'interférence.
revient à une mesure de visibilité de la figure d'interférence.

 , sur une base
, sur une base  . L'autocorrélation de la pupille donne accès aux hautes fréquences spatiales
. L'autocorrélation de la pupille donne accès aux hautes fréquences spatiales 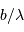 .
.
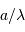 , et donnant une résolution angulaire de
, et donnant une résolution angulaire de 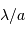 .
.
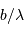 ; sa résolution angulaire est
; sa résolution angulaire est 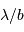 .
.
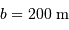 apporte à
apporte à 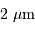 une résolution angulaire de :
une résolution angulaire de :
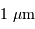 , sera résolue pour une base de :
, sera résolue pour une base de :

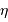 du Bouvier.
du Bouvier.

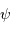 de la constellation du Phénix.
de la constellation du Phénix.

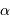 de la constellation d'Hercule.
de la constellation d'Hercule.

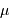 de Céphée.
de Céphée.
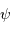 Phe et
Phe et 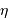 Boo.
Boo.
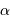 d'Hercule
d'Hercule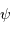 Phe,
Phe, 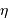 Boo et
Boo et 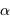 Her sont estimées à respectivement 10.1, 88.2, 8.5 mas. En déduire la distance de chaque étoile, puis son diamètre linéaire.
Her sont estimées à respectivement 10.1, 88.2, 8.5 mas. En déduire la distance de chaque étoile, puis son diamètre linéaire.
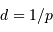 donne directement la distance en parsec si la parallaxe
donne directement la distance en parsec si la parallaxe 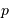 est mesurée en seconde d'arc.
est mesurée en seconde d'arc.
 Cep
Cep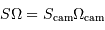 donne un angle solide objet
donne un angle solide objet
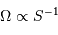
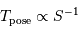
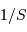 , la surface collectrice. Le temps de pose élémentaire varie comme
, la surface collectrice. Le temps de pose élémentaire varie comme 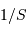 . Pour couvrir un champ donné, la durée totale ne dépend donc pas de la taille du télescope : le champ couvert en 1 pose de durée
. Pour couvrir un champ donné, la durée totale ne dépend donc pas de la taille du télescope : le champ couvert en 1 pose de durée 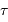 avec un petit collecteur sera observée par
avec un petit collecteur sera observée par 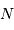 poses de durées
poses de durées 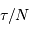 avec un grand.
avec un grand.

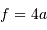 . L'étendue du faisceau s'écrit dont de 2 façons différentes, selon que l'on considère le montage réel ou le montage équivalent :
. L'étendue du faisceau s'écrit dont de 2 façons différentes, selon que l'on considère le montage réel ou le montage équivalent :
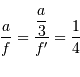
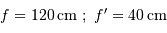

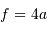 .
.
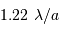 , couvre un angle solide de l'ordre de :
, couvre un angle solide de l'ordre de :
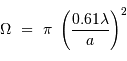
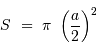
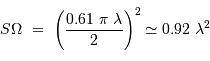
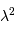 .
.
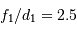 , la lentille L2 sous
, la lentille L2 sous 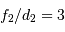 .
.
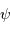 Phe : 1/147 = 6.8 mas
Phe : 1/147 = 6.8 mas
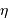 Boo : 1/61 = 16.4 mas
Boo : 1/61 = 16.4 mas
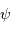 Phe : 99 pc,
Phe : 99 pc, 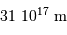 .
.
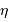 Boo : 11 pc, 3.5 ...
Boo : 11 pc, 3.5 ...
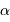 Her : 118 pc, 36 ...
Her : 118 pc, 36 ...
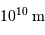 , puis en diamètre solaire et unité astronomique :
, puis en diamètre solaire et unité astronomique :
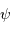 Phe : 10.4, soit 74 fois le diamètre solaire, ou 0.70 UA.
Phe : 10.4, soit 74 fois le diamètre solaire, ou 0.70 UA.
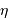 Boo : 2.9, ... 20.5 ... 0.19
Boo : 2.9, ... 20.5 ... 0.19
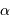 Her : 42, ... 300 ... 2.8
Her : 42, ... 300 ... 2.8
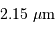 mais opaque à
mais opaque à 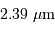 .
.