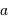 et de fréquence
et de fréquence 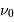 , la définition donne :
, la définition donne :
Avec un signal purement sinusoïdal d'amplitude 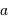 et de fréquence
et de fréquence 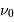 , la définition donne :
, la définition donne :
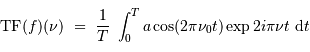
Pour 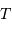 grand devant
grand devant 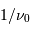 , si
, si 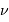 est différent de
est différent de 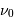 , l'intégrale tend vers 0, alors que pour
, l'intégrale tend vers 0, alors que pour 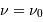 , on retrouve :
, on retrouve :
![\mathrm{TF} (f) (\nu_0) \ =\ {1\over T}\ \int_0^T {a\over 2} [\exp 2i\pi \nu_0 t + \exp -2i\pi \nu_0 t]\ \exp 2i\pi \nu_0 t \ {\mathrm{d}} t \ ={1\over T}\ \int_0^T {a\over 2} \ {\mathrm{d}} t \ = {a\over 2}](../pages_traiter/equations_analyse-tf/equation44.png)
Au facteur 1/2 près, dû au fait que la TF en 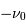 est également non nul,
la normalisation en
est également non nul,
la normalisation en 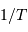 par rapport à la définition de la TF usuelle permet de retrouver dans le spectre l'amplitude du signal sinusoïdal.
par rapport à la définition de la TF usuelle permet de retrouver dans le spectre l'amplitude du signal sinusoïdal.