
|
Approche mathématique de la transformation de Fourier
Présentation de la transformation de Fourier, et rappel de quelques propriétés.
La transformation de Fourier associe à une fonction 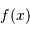 sa transformée~:
sa transformée~:
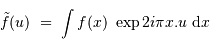
Les variables 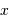 et
et 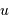 sont conjuguées. A la variable temporelle
sont conjuguées. A la variable temporelle 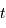 est associée la variable fréquentielle
est associée la variable fréquentielle 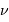 ; à la variable d'espace
; à la variable d'espace 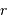 , la fréquence spatiale
, la fréquence spatiale 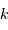 .
.
La TF est dotée de multiples propriétés (linéarité...) : se référer à un cours de maths.
L'opération inverse de la TF est notée :
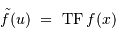 et
et
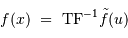 .
.
Il ne s'agit rien d'autre que de la conservation de l'énergie, qui ici s'exprime par :
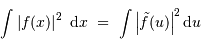
Autrement dit, l'énergie d'un signal ne peut pas dépendre de la description de ce signal, directe ou fréquentielle.
| grandeur | notation | unité | exemple |
|---|---|---|---|
| variable | 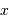 |
X | temps, en s |
| variable conjuguée | 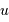 |
1/X | fréquence, en Hz |
| signal | 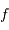 |
Y | vitesse, en m/s |
| spectre | 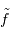 |
XY | m |
| spectre d'amplitude | 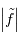 |
XY | m |
| spectre de puissance | 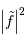 |
![[\mathrm{XY}]^2](../pages_traiter/equations_analyse-tf/equation18.png) |
 |
La définition de la transformation, continue, se doit d'être amendée pour tenir compte du fait qu'un signal réel est échantillonné. L'analyse de Fourier discrète s'appuie sur un nombre fini de réalisations du signal, et donne un nombre finie de fréquences pour le décrire. La discrétisation s'opère en douceur, car la TF d'une fonction peigne (succession équidistance de Dirac), fonction retranscrivant l'échantillonnage du signal, est une fonction peigne.
L'analyse de Fourier rapide (fast Fourier transform, ou FFT) est une une forme spécifique de programmation de la transformation de Fourier. Une routine de calcul fft est présente dans toute bonne bibliothèque de programmation.
L'usage d'une FFT implique:
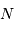 tel que
tel que 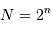 points, sinon le gain en temps est annulé, et la FFT peut
devenir
extrêmement lente si le nombre de points est premier, ou se
factorise avec de grands facteurs premiers.
points, sinon le gain en temps est annulé, et la FFT peut
devenir
extrêmement lente si le nombre de points est premier, ou se
factorise avec de grands facteurs premiers.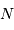 valeurs conduit à un spectre de
valeurs conduit à un spectre de 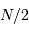 fréquences.
fréquences.