
|
Difficulté : ☆☆ Temps : 40 min
Vérifier l'homogénéité de la conservation de l'énergie énoncée par le théorème de Parseval-Plancherel.
Pour des raisons physiques, il est commode de poser la définition de la TF d'une série temporelle bornée sur un intervalle de temps 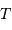 comme :
comme :
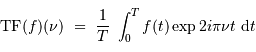
avec le changement de notation pour préciser la différence par rapport à la TF classique. Montrer l'intérêt physique de cette notation, en s'appuyant p.ex. sur un signal purement sinusoïdale.
Pour d'autre raisons, il peut être commode de poser la définition de la TF d'une série temporelle discrète d'une manière différente :
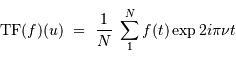
avec le changement de notation pour préciser la différence par rapport à la TF classique. Réécrire la relation de Parseval-Plancherel, et montrer que
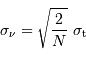
où 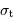 et
et 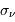 sont respectivement les écarts-types de la série temporelle et du spectre.
sont respectivement les écarts-types de la série temporelle et du spectre.