|
Flux de Poisson et d'Erlang
Date de création : 23/05/2003
Auteur: Didier Pelat
Introduction
Cette démonstration simule l'arrivée d'événements constituant un flux de Poisson ou, plus généralement, un flux d'Erlang
Les événements sont repérés par un "bip" sonore.
Au fur et à mesure que les événements arrivent, la fonction de répartition empirique est construite.
Un flux d'Erlang est caractérisé par deux paramètres : 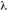 ( lambda ) et  ( nu ), 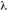 est le taux moyen d'arrivée des événements et  permet de transformer un flux de Poisson en un flux d'Erlang.
Pour un flux de Poisson,  est toujours égal à un.
De nombreux événements de la vie courante peuvent être assimilés aux événements d'un flux de Poisson ou d'Erlang. Les pannes sur une chaîne de fabrication, les événements fortuits heureux ou malheureux qui arrivent dans une vie, la désintégration radioactive alpha.
Il faut bien peu d'hypothèses pour que des événements puissent être considérés comme formant un flux de Poisson, d'où la très grande importance de ce modèle.
Liste des paramètres de l'applet
-
label : lambda
type : nombre
titre : taux moyen d'arrivée des événements
unités : nombre d'événements par unité de temps
Lorsque l'on active la démonstration, lambda est mis à une valeur telle que le taux d'arrivée des événements soit d'environ un événement par seconde.
Cette valeur peut varier d'un utilisateur à un autre, de plus, elle est susceptible d'évoluer avec les performances des processeurs.
Si on multiplie lambda par deux, par exemple, les bips sonores se succéderons alors à un rythme moyen deux fois plus rapide.
-
label : nu
type : nombre
titre : intervalle entre deux évenements retenus
unités : nombre d'événements
La valeur de nu n'a de sens que pour un flux d'Erlang, elle est ignorée si on choisit de simuler un flux de Poisson.
Pour construire un flux d'Erlang, on part d'un flux de Poisson et on ne retient qu'un événements tous les nu. Si par exemple nu=4 les 3 premiers événements poissoniens sont ignorés et le quatrième est retenu.
Ainsi les événements poissoniens portant les numéros 4, 8, 12 etc. forment le flux d'Erlang de paramètre nu=4.
Il est possible de donner un valeur non entière à nu mais le flux ainsi créé ne s'interprète pas si simplement à partir d'un flux de Poisson.
-
label : tcl
type : string
titre : affiche ou non la limite gaussienne équivalente
Cette case à cocher permet de visualiser la limite donnée par la loi de Gauss.
Dans un premier temps, il est recommandé de laisser cette case décochée.
-
label : demo
type : string
titre : Type de flux d'événements
Le bouton "flux" permet de choisir entre trois types de flux :
un flux de Poisson de paramètre lambda ; un flux d'Erlang de paramètres lambda et nu enfin un flux d'Erlang de paramètres lambda*nu et nu.
Etant donné que le nombre moyen de "bips" est de lambda/nu pour un flux d'Erlang, l'option "Erlang*nu" permet d'entendre autant de "bips" en moyenne que pour le flux de Poisson de même lambda.
Mode d'emploi de l'applet
Finalement le bouton "flux d'Erlang" lance la démonstration.
Exemple d'utilisation
Dans ce premier exemple, on laissera les paramètres par défaut ou on les rétablira en cliquant sur le bouton "Réinitialiser".
lorsqu'on lance la démonstration, il se passe alors plusieurs choses :
- Un "bip" est émis à l'arrivée de l'événement.
Le nombre de bips émis depuis de début est indiqué en bas du graphique sous le nom "nb de points".
- Le temps qu'il a fallu attendre avant l'arrivée de cet événement est indiqué en bas du graphique sous le nom de "dernière tempo".
Ce temps est donné en millisecondes.
- Un repère représentant l'événement est tracé sur le graphique.
Ses coordonnées sont, en x : le temps d'attente en millisecondes et en y : la proportion des événements déjà arrivés dont le temps d'attente a été inférieur ou égal au temps qu'il a fallu attendre l'événement actuel.
- La fonction de répartition empirique est construite au fur et à mesure de l'arrivée des événements.
Cette fonction "en escalier", ici en bleu, est la proportion des événements dont la durée d'attente est inférieure ou égale au temps indiqué par l'axe des x.
On trouvera en rouge la fonction de répartition théorique du flux de Poisson, c'est-à-dire la probabilité pour que le temps d'attente entre deux événements ne soit pas plus long que le temps indiqué par l'axe des x.
Remarque :
Notez qu'il sera peut-être nécessaire de cliquer sur le bouton "ajuster" afin de mettre le graphique à l'échelle.
Au cours du déroulement de cette démonstration, on remarquera peut-être qu'il y a de longs moments de silence suivis par une série de "bips" rapprochés.
Il en va effectivement ainsi des événements d'un flux de Poisson, ils arrivent le plus souvent groupés.
En effet, la densité de probabilité des temps séparant deux événements est une exponentielle décroissante, son mode est en zéro, cela veut bien dire que, le plus souvent, les événements arrivent les uns derrière les autres ( ne dit-on pas d'ailleurs "un malheur n'arrive jamais seul" ou "jamais deux sans trois" ? ).
On constatera également que la courbe empirique bleue converge vers la courbe théorique rouge.
Cette convergence est une convergence stochastique, c'est-à-dire qu'elle n'a de sens qu'en probabilité.
En fait il s'agit là d'une illustration du théorème de Glivenko-Cantelli qui dit que la fonction de répartition empirique ainsi calculée converge presque-sûrement et uniformément vers la fonction de répartition théorique.
Ce résultat est d'une importance capitale en statistique.
On obtiendra une convergence beaucoup plus spectaculaire si on augmente lambda d'un facteur 100, par exemple, et que l'on relance la démonstration.
Exemple d'utilisation
Dans cet exemple, on va augmenter lambda d'un facteur 100 de façon à accélérer la convergence de la courbe empirique vers la courbe théorique.
A cette fin on rétablira les valeurs par défaut et on remplira la case "lambda" avec une valeur correspondant à la valeur par défaut multipliée par cent et on relancera la démonstration.
Il sera éventuellement nécessaire d'ajuster l'échelle du graphique à l'aide de la case appropriée.
On constate que très rapidement la courbe bleue tend à se confondre avec la courbe rouge, cependant les deux courbes ne sont jamais partout confondues.
Il est facile de s'en rendre compte en agrandissant une zone quelconque, pour cela il faut cliquer avec le curseur au point supérieur gauche du carré à agrandir puis de le relâcher au point inférieur droit.
En zoomant ainsi de façon successive on se rend compte de la distance entre les deux courbes.
Cette distance est une variable aléatoire dont la moyenne est nulle et dont la variance est proportionnelle au nombre d'événements.
De nouveau, comme c'est souvent le cas en statistique, les fluctuations de la valeur empirique autour la valeur théorique sont de l'ordre de grandeur de la racine carrée de la taille de l'échantillon.
Cette démonstration pouvant être très longue, on l'arrêtera à l'aide du bouton "stop".
Remarque :
On constatera que lorsque le nombre de points devient très grand, le flux d'événements ralentit.
Cela est dû au temps nécessaire pour afficher un graphique de plus en plus complexe, notre simulation est alors en défaut, lambda n'est plus constant. Il s'agit alors d'un flux de Poisson non-stationnaire.
Exemple d'utilisation
On se propose maintenant de simuler un flux d'Erlang de paramètres lambda et nu.
On conservera la valeur lambda du flux de Poisson et on prendra nu=4.
On rappelle qu'un point sur nu du Flux de Poisson est conservé dans le flux d'Erlang, les autres sont effacés.
L'effet de cet effacement est de rendre la succession des événements beaucoup plus régulière, les événements arrivent beaucoup moins groupés qu'au sein d'un flux de Poisson.
Afin de rentre plus évident cette différence de comportement, on lancera la démonstration avec l'option "erlang*nu" dans la case flux:
Avec cette option, le lambda de Poisson est multiplié par nu de façon à ce que le taux moyen d'événements soit le même que pour le flux de Poisson original.
Avant de lancer la démonstration, on décochera la case "Gauss limit".
|