Histogramme d'une loi de Poisson
Date de création : 12/01/2004
Auteur: Didier Pelat
Introduction
Cette démonstration introduit la notion d'histogramme d'un échantillon, elle montre de plus que la moyenne arithmétique de cet histogramme converge vers un histogramme théorique.
A partir d'un échantillon de Poisson (voir la démonstration "Bruit de Poisson") on construit un histogramme en portant en abscisse les issues possibles de la variable aléatoire et en ordonnée le nombre de fois où cette variable a été obtenue dans l'échantillon.
Pour les variables aléatoire discrètes, comme le cas de Poisson, il n'y a pas d'autres considérations pour construire l'histogramme.
Pour les variables aléatoires continues il faut définir des intervalles (des classes) ce qui introduit un certain arbitraire, en général on évite de considérer les histogrammes de variables aléatoires continues.
Si on réalise la moyenne arithmétique des histogrammes, chaque classe est soumise à la loi des grands nombres et converge vers la moyenne de la classe qui est classiquement la probabilité de l'issue qui correspond à la classe.
Par exemple, dans le cas de variables de Poisson, la moyenne arithmétique du nombre de fois où on a obtenu 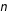 converge vers une valeur qui est prévue par des considérations théoriques.
Cette valeur est :
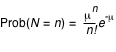 , où 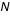 est la variable de Poisson et  sa moyenne.
Pour 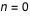 , par exemple, on obtient 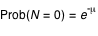 , soit pour 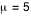 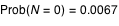 environ.
Liste des paramètres de l'applet
-
label : mu
type : nombre
titre : moyenne de la loi de Poisson
unités : sans dimensions
Cette case permet de préciser la moyenne de la variable de Poisson que l'on désire étudier par défaut elle vaut cinq.
-
label : npts
type : nombre
titre : taille de l'échantillon dont on fait l'histogramme
unités : nombre entier positif
Ici on précise la taille de l'échantillon, il vaut trente par défaut.
-
label : distrib
type : string
titre : affiche ou non la probabilité attachée à l'issue N=n
Cette case à cocher permet de visualiser l'histogramme théorique de la loi de Poisson de moyenne mu.
Dans un premier temps, il est recommandé de laisser cette case décochée.
-
label : tcl
type : string
titre : affiche ou non la loi de Gauss de même moyenne et de même écart type
Cette case à cocher permet de visualiser la densité de probabilité de l'approximation gaussienne de même moyenne et écart type.
Dans un premier temps, il est recommandé de laisser cette case décochée.
Mode d'emploi de l'applet
La démonstration est lancée à l'aide de trois boutons :
- Le bouton "bruit de Poisson-histogramme" affiche en rouge l'histogramme empirique obtenu à l'aide de l'échantillon de la taille sélectionnée (30 si on a laissé les valeurs par défaut).
- Le bouton "moyenne" montre la convergence de la moyenne arithmétique des histogrammes empiriques vers l'histogrammme théorique.
- Le bouton "tableau" présente un l'échantillon de Poisson sous la forme d'un tableau à deux colonnes.
La colonne "hx" est la valeur de la variable aléatoire et la colonne "hy" est le nombre de fois où cette valeur a été observée dans l'échantillon.
Exemple d'utilisation
Cet exemple va nous permettre de nous familiariser avec la forme d'un d'histogramme d'une variable de Poisson. Cette forme varie beaucoup avec la valeur de la moyenne surtout quand elle est petite.
Dans un premier temps on laisse les valeurs par défaut et on décoche les cases "distribution" et "Gauss limit".
On lance la démonstration en cliquant sur "bruit de Poisson-histogramme".
On obtient un histogramme rouge qui représente le nombre de fois où des valeurs entières positives ou nulles.
En principe il n'y a pas de borne supérieure, une variable de Poisson peut-être aussi élevée que l'on veut.
On peut obtenir d'autres histogrammes empiriques en cliquant sur "Relancer" autant de fois que l'on veut
On devrait constater que, par exemple, on obtient au moins un zéro deux fois sur dix environ (si on a bien conservé les valeurs par défaut).
Nous allons changer la valeur de  en cliquant sur la barre "Réinitialiser" et en donnant la valeur 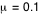 par exemple.
On cochera la case "distribution" et on décochera la cas "Gauss limit".
On lance de nouveau la démonstration en cliquant sur "bruit de Poisson-histogramme".
On constatera que la plupart du temps on obtient 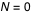 ou 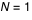 et très rarement des valeurs supérieures ou égales à deux.
Ce comportement est conforme à la propriété des flux de Poisson d'être séparables : la probabilité d'obtenir deux événements ou plus dans un temps donné tend vers zéro quand l'intervalle de temps approche de zéro.
On constate aussi que l'histogramme théorique, en bleu, donne une probabilité très faible pour deux et au delà.
Maintenant on illustre le comportement d'une variable de Poisson lorsque sa moyenne  devient grande.
Pour cela on va choisir 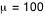 et on laissera toutes les cases cochées.
On constate que l'histogramme théorique en bleu s'approche d'une courbe en cloche et peut être approché par un histogramme calculé à partir d'une loi normale de même moyenne et de même écart type
intégré sur des classes correspondant à des nombres entiers.
L'histogramme empirique en rouge semble s'écarter de la valeur théorique, ce qui est normal pour un échantillon de taille si faible.
Pour avoir une meilleure impression visuelle, on peut augmenter la taille de l'échantillon à 300 par exemple.
Exemple d'utilisation
Cette démonstration illustre la convergence de la moyenne arithmétique des histogrammes empiriques vers l'histogramme théorique.
On rétablira au besoin les valeurs par défaut et on lance la simulation en cliquant sur "moyenne".
On lance ainsi une série de 400 itérations.
En bleu on a l'histogramme obtenu par des considérations théoriques et en rouge les moyennes arithmétiques successives pour chaque valeurs de l'histogramme.
Ces valeurs sont des variables aléatoires qui, d'après la loi des grands nombres, doivent converger vers leur moyenne (a condition qu'elle existe, ce qui est le cas ici).
Cette valeur vers laquelle on converge est la définition classique de la probabilité (on dit aussi "fréquentiste").
La courbe continue en bleu pâle est la densité de probabilité d'une variable aléatoire normale (ou de Gauss) de même moyenne et de même écart type et mise à l'échelle de façon à ce que son intégrale soit égale à la taille de l'échantillon.
On peut relancer la simulation avec 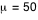 , par exemple, sans oublier de cliquer éventuellement sur "ajuster" afin de voir la courbe.
|