Calcul de géodésiques autour d'un trou noir de SchwarzschildAuteur: COUETDIC JocelynAuteur: DUMAS Gaëlle Auteur: FERRAND Gilles Date de création : 24/02/04
Date de mise à jour : 08/03/04
IntroductionLe but de cette appliquette JAVA est de calculer et tracer des géodésiques autour d'un trou noir. On ne tracera que des géodésiques venant d'une direction à l'infini avec un paramètre d'impact b. En effet, par principe de retour inverse de la lumière, cela équivaut à calculer et tracer les trajectoires des photons qui voyagent depuis le voisinage du trou noir (émis par exemple par un disque d'accrétion) vers la plaque photographique d'un observateur. L'utilisateur peut ainsi entrer une valeur du paramètre d'impact et voir le tracé de la géodésique correspondante à l'écran, ainsi que l'angle de déviation et le nombre de tours autour du trou noir de la trajectoire.Rappels de coursLa physique sous-jacente est expliquée dans le cours Images et spectre d'un disque fin autour d'un trou noirMode d'emploi de l'appletOn montre que l'équation vérifiée par ces géodésiques r( ) ne dépend que du paramètre d'impact (et de la masse du trou noir) : ) ne dépend que du paramètre d'impact (et de la masse du trou noir) : 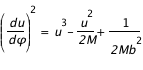 . Le programme intègre donc numériquement une géodésique pour une valeur de b donnée. Cette intégration se fait au moyen d'un algorithme de type Runge-Kutta d'ordre 4. Pour plus de détail sur cette intégration le lecteur pourra se reporter à la section 'Explications'. . Le programme intègre donc numériquement une géodésique pour une valeur de b donnée. Cette intégration se fait au moyen d'un algorithme de type Runge-Kutta d'ordre 4. Pour plus de détail sur cette intégration le lecteur pourra se reporter à la section 'Explications'.
Tracé d'une géodésique
L'observateur est en O' et le trou noir en O. L'applet trace r(
 ) pour un b donné ) pour un b donné
Crédit : Gilles FERRAND Trois scénarios pour la trajectoire sont possibles :
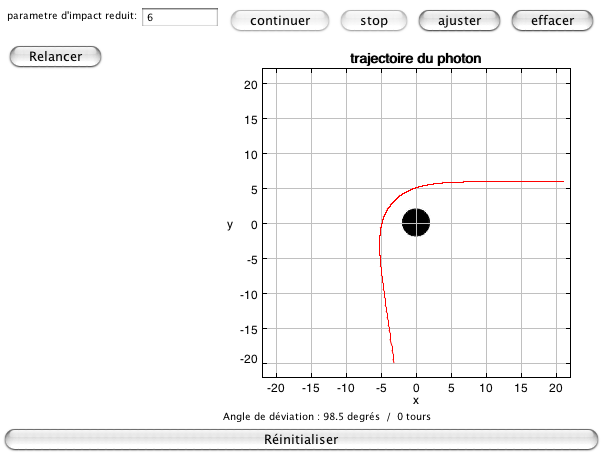
Dans les deux premiers cas de figure, la trajectoire peut s'enrouler plusieurs fois autour du trou noir. L'applet calcul ce nombre de tours en comptant les passages à 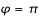 (le premier excepté). On s'aperçoit que la valeur critique du paramètre d'impact donne lieu à une trajectoire qui s'échappe après un peu plus de 3 tours et demi. Il faut noter qu'en plus des erreurs de l'intégrateur, la valeur de b utilisée par l'algorithme ne peut être qu'un rationnel aussi près que possible de la vraie valeur compte tenu de la précision disponible (10-15 ici). (le premier excepté). On s'aperçoit que la valeur critique du paramètre d'impact donne lieu à une trajectoire qui s'échappe après un peu plus de 3 tours et demi. Il faut noter qu'en plus des erreurs de l'intégrateur, la valeur de b utilisée par l'algorithme ne peut être qu'un rationnel aussi près que possible de la vraie valeur compte tenu de la précision disponible (10-15 ici).
Géodésique pour le paramètre critique
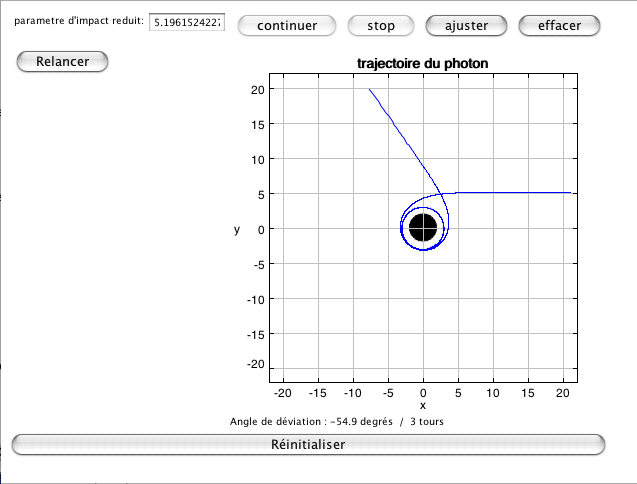
Crédit : Jocelyn COUETDIC Exemple d'utilisation
allures des géodésiques
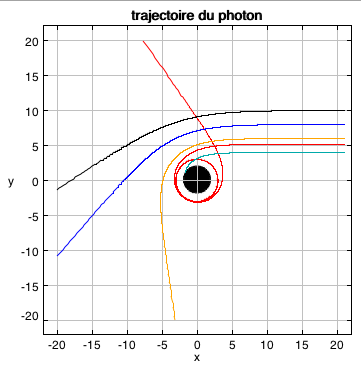
Différentes géodésiques pour différents paramètres d'impacts: 4,
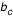 , 6, 8, 10. On voit bien les deux comportements des géodésiques suivant la valeur de b, supérieure ou inférieure au paramètre critique. , 6, 8, 10. On voit bien les deux comportements des géodésiques suivant la valeur de b, supérieure ou inférieure au paramètre critique.
Crédit : Jocelyn COUETDIC Liste des paramètres de l'applet
Explications
Nous avons vu que nous souhaitions intégrer l'équation (avec M=1) :
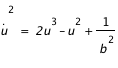 . Ce n'est pas très judicieux car nous devrons calculer une racine pour obtenir . Ce n'est pas très judicieux car nous devrons calculer une racine pour obtenir 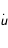 , ce qui pose des problèmes pour la détermination du signe. On a en effet deux solutions et il faut passer de l'une à l'autre au périastre de la trajectoire !! On préfère donc dériver cette équation pour obtenir : , ce qui pose des problèmes pour la détermination du signe. On a en effet deux solutions et il faut passer de l'une à l'autre au périastre de la trajectoire !! On préfère donc dériver cette équation pour obtenir :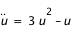 si si 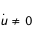 . On a maintenant une équation différentielle du deuxième ordre qui est juste fausse au périastre. On passe alors en général à un système double du premier ordre : . On a maintenant une équation différentielle du deuxième ordre qui est juste fausse au périastre. On passe alors en général à un système double du premier ordre :
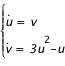
Ce système du type
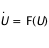 s'intègre facilement avec une méthode comme Runge-Kutta d'ordre 4. Le principe est de calculer à chaque pas d'intégration de taille s'intègre facilement avec une méthode comme Runge-Kutta d'ordre 4. Le principe est de calculer à chaque pas d'intégration de taille  . .
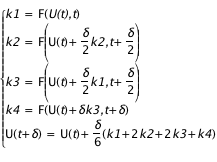
L'idée des méthodes de type Runge-Kutta consiste à estimer l'incrément avec différentes valeurs de la dérivé en différents points (eux aussi estimés) situés entre le point actuel U(t) et le point recherché U(t+
 ). Ces dérivés sont modulées par des coefficients, et la position des points intermédiaires est aussi paramétrée par d'autres coefficients. A l'ordre 4 on utilise donc quatre dérivés. Le choix des valeurs des différents coefficients et poids exprimé dans le système d'équations est celui le plus couramment utilisé. ). Ces dérivés sont modulées par des coefficients, et la position des points intermédiaires est aussi paramétrée par d'autres coefficients. A l'ordre 4 on utilise donc quatre dérivés. Le choix des valeurs des différents coefficients et poids exprimé dans le système d'équations est celui le plus couramment utilisé.
|
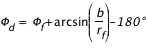
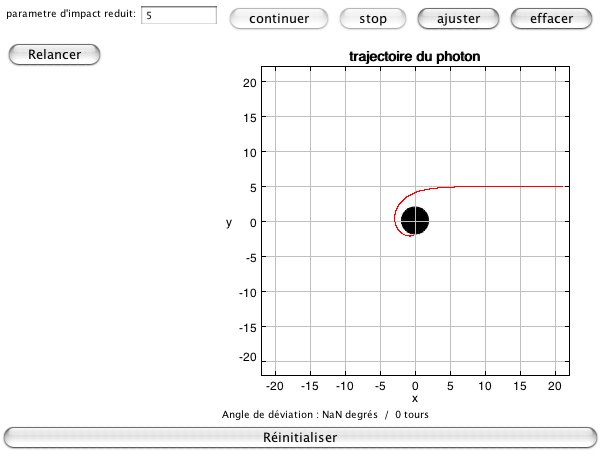
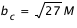 . Pour un paramètre d'impact plus petit que la valeur critique, il y a capture, et sinon il y a échappement
. Pour un paramètre d'impact plus petit que la valeur critique, il y a capture, et sinon il y a échappement