
 Croissance «ordonnée» d'une population de planétésimaux
Croissance «ordonnée» d'une population de planétésimaux
Comme nous l’avons vu (cf. lien1 et lien2 ), l’étape intermédiaire dans le scénario de formation planétaire est celle qui fait passer de planétésimaux kilométriques à des « embryons » planétaires de 500-1000km. Lors de cette étape, le processus fondamental est l’attraction gravitationelle mutuelle des planétésimaux lors de leurs rencontres. Dans sa version initiale, le modèle d’accrétion des planétésimaux supposait que ceux-ci croissent de manière « ordonnée », c’est à dire tous ensemble et à la même vitesse. Même si on sait qu’aujourd’hui ce scénario ne correspond pas à la réalité (l’accrétion se faisant par effet « boule de neige » bien plus rapide), il est quand même intéressant d’avoir une idée du rythme de croissance pour cette croissance « ordonnée ».
Question 1)
Pouvez vous ainsi estimer le temps qu’il faut pour former des corps de 1000km à partir d’une population de corps de 1km ? On supposera que :
- On se situe à 1UA dans une Nébuleuse Solaire de Masse Minimale (cf. cours et Exercice 2).
- Le disque de planétésimaux est toujours à l’équilibre dynamique, à savoir que les vitesses de rencontres
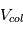 sont de l’ordre des vitesses de libération
sont de l’ordre des vitesses de libération 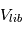 (attention :
(attention : 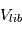 va donc évoluer au cours du temps, car cette vitesse est directement proportionnelle à la taille des planétésimaux)
va donc évoluer au cours du temps, car cette vitesse est directement proportionnelle à la taille des planétésimaux) - Les orbites des planétésimaux sont orientées de manière totalement aléatoire.
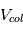 peut alors facilement s’exprimer en fonction de l’excentricité des orbites (voir cours).
peut alors facilement s’exprimer en fonction de l’excentricité des orbites (voir cours). - Il y a « équipartition » entre les composantes planes et verticales des orbites des planétésimaux, c’est à dire concrètement que leur inclinaison i = ½ e.
- Chaque rencontre entre planétésimaux se traduit par l’accrétion de ces corps l’un sur l’autre
- Tous les planétésimaux grandissent ensemble et au même rythme, c’est à dire qu’à tout instant ils ont tous la même taille
- Dans la MMSN, la densité surfacique de matière solide à 1UA est σ ∼ 10g/cm2
- La densité massique d'un planétésimal est comparable à celle d'un astéoïde, soit environ 3g/cm3
AideSolution
On peut commencer par estimer, pour un planétésimal de taille r, quel est le nombre d’autres planétésimaux (de même taille r) qu’il va rencontrer par unité de temps. Pour cela, on peut supposer que ce planétésimal avance en ligne droite à la vitesse 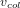 dans un disque d’épaisseur
dans un disque d’épaisseur 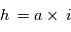 (où a est la distance au soleil eti est l'inclinaison des orbites de tous les planétésimaux)
(où a est la distance au soleil eti est l'inclinaison des orbites de tous les planétésimaux)
Pendant un temps dt, un planétésimal balaye le volume 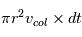 .
Il faut maintenant estimer le nombre de planétésimaux contenus en moyenne dans ce volume.
Ce nombre est donné par
.
Il faut maintenant estimer le nombre de planétésimaux contenus en moyenne dans ce volume.
Ce nombre est donné par 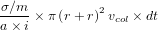 (m étant
la masse d'un planétésimal). Le terme en (r + r)2 vient du fait que
même des corps dont le centre n'est pas dans le volume balayé par le planétésimal considéré
peuvent être impactés par lui en raison de leur taille non-nulle r.
En remplaçant vcol par e.vKep, e/i par 2 et
m par 4/3ρπr3 on obtient un taux
de collision de
(m étant
la masse d'un planétésimal). Le terme en (r + r)2 vient du fait que
même des corps dont le centre n'est pas dans le volume balayé par le planétésimal considéré
peuvent être impactés par lui en raison de leur taille non-nulle r.
En remplaçant vcol par e.vKep, e/i par 2 et
m par 4/3ρπr3 on obtient un taux
de collision de 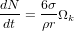 , où Ωk est la vitesse angulaire orbitale. Comme on suppose
que tous les planétésimaux ont toujours la même taille, on a donc, qu'à chaque collision, le
planétésimal accrète 1 fois sa propre masse. Donc
, où Ωk est la vitesse angulaire orbitale. Comme on suppose
que tous les planétésimaux ont toujours la même taille, on a donc, qu'à chaque collision, le
planétésimal accrète 1 fois sa propre masse. Donc 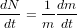 , ce qui donne, en remplaçant dN/dt par la formule précédente et (1/m)*(dm/dt) par (3/r)*(dr/dt), la formule
, ce qui donne, en remplaçant dN/dt par la formule précédente et (1/m)*(dm/dt) par (3/r)*(dr/dt), la formule 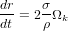 .
On remarque que cette formule très simple ne dépend ni de e, ni de i,
ni de la taille des planétésimaux.
Et, à 1UA, cela donne un taux de croissance
.
On remarque que cette formule très simple ne dépend ni de e, ni de i,
ni de la taille des planétésimaux.
Et, à 1UA, cela donne un taux de croissance 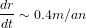 , soit environ 2.5 millions d'années pour
former un corps de 1000km.
, soit environ 2.5 millions d'années pour
former un corps de 1000km.

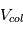 sont de l’ordre des vitesses de libération
sont de l’ordre des vitesses de libération 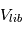 (attention :
(attention : 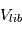 va donc évoluer au cours du temps, car cette vitesse est directement proportionnelle à la taille des planétésimaux)
va donc évoluer au cours du temps, car cette vitesse est directement proportionnelle à la taille des planétésimaux)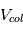 peut alors facilement s’exprimer en fonction de l’excentricité des orbites (voir cours).
peut alors facilement s’exprimer en fonction de l’excentricité des orbites (voir cours).