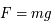Apprendre

Prérequis

Relation fondamentale de la dynamique ; notion de référentiel galiléen

La force d'interaction gravitationnelle

Définition

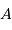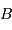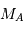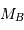L'interaction gravitationnelle entre deux corps et de masse M_A et M_B , séparés par la distance $r_{AB}$ :

est colinéaire à la direction AB
est attractive
se traduit par une force, de A sur B, opposée à celle de B sur A, égale algébriquement à :

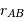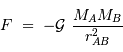
$F\ =\ - { {\mathcal{G}}}\ {M_A M_B \over r_{AB}^{2}}$

Le potentiel gravitationnel

Un objet sphérique de masse 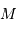, rayon 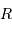, crée un potentiel gravitationnel :

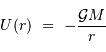
$U(r)\ =\ - { {\mathcal{G}} M\over r}$

Cette expression suppose implicitement un potentiel nul à l'infini. Cette convention, arbitraire comme toute convention, peut se justifier par divers arguments :

Le modèle suppose l'absence de toute masse perturbatrice à proximité.
L'histoire des corps condensés de l'Univers débute dans un état de matière très dilué, tellement plus dilué que l'état condensé final que l'on peut considérer les constituants initialement à l'infini, càd très éloignés les uns des autres.
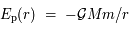
Argument a posteriori : on peut ainsi distinguer un système gravitationnellement lié par son énergie mécanique totale négative. Séparer le système nécessite de lui apporter une énergie qui contrebalance cette énergie de liaison $E _{\mathrm{p}}(r) \ =\ - { {\mathcal{G}} Mm/ r}$

Invariants

Il est commode de traduire les spécificités d'un problème physique en termes de grandeurs invariantes.

Champ de force : L'interaction gravitationnelle correspond, comme toute interaction fondamentale, à un champ de force. A ce champ de force est associé un potentiel. La conservation de l'énergie mécanique en découle.
Force centrale : Le moment d'une force centrale est nul au centre de force. La conservation du moment cinétique en découle.
Champ de force central variant comme l'inverse du carré de la distance : Cette forme spécifique du champ de force introduit un 3e invariant, le vecteur excentricité, qui définit la trajectoire. Un exercice explicite ceci.

On peut ajouter un autre invariant, pour un système supposé isolé, la conservation de la quantité de mouvement totale du système.

Potentiel, énergie, force, champ

Quatre termes rendent compte de la même réalité, avec quatre dimensions différentes. L'énergie potentielle gravitationnelle est bien évidemment une énergie, et la force gravitationnelle une force.

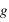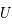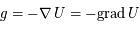Le champ gravitationnel dérive du potentiel gravitationnel via $g = - \nabla\, U = - \mathrm{grad} \, U$ , où l'opérateur gradient désigné la dérivation par rapport à l'ensemble des coordonées spatiales. En coordonnées sphérique, dans un problème à symétrie sphérique,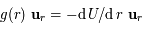 $g(r) \ \mathbf{u}_r = - \mathrm{d}\, U / \mathrm{d}\, r \ \mathbf{u}_r$
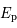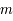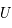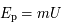
L'énergie gravitationnelle $E _{\mathrm{p}}$ d'un corps de masse dans un potentiel gravitationnel vaut $E _{\mathrm{p}} = m U$
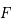La force gravitationnelle subie par un corps de masse 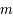dans un champl gravitationnel 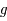vaut