Rappel sur les excentriques, épicycle et mettre le schéma
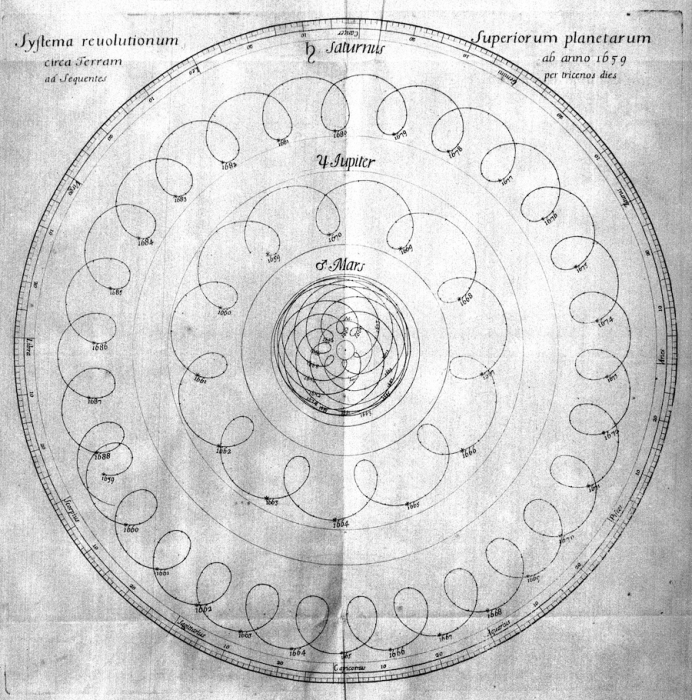
épicycles
Crédit :
Bibliothèque de l'Observatoire de Paris
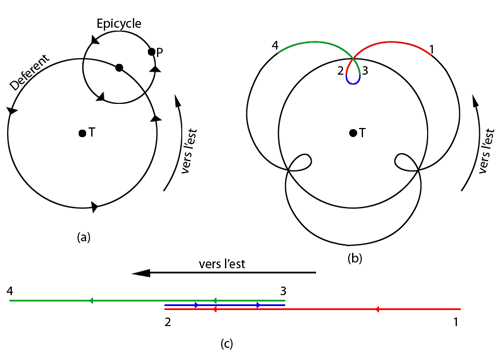
Combinaison d'un cercle déférent et d'un épicycle (a). Mouvement de la planète P autour de la Terre (b). Parties 1, 2, 3, 4 du mouvement décrit en (b), tel qu'il serait vu depuis la Terre (c).
Crédit :
Jérôme Lamy et Gilles Bessou Observatoire de Paris
Point équant
Difficulté : ☆☆
Question 1)
Vous détaillerez brièvement la théorie des excentriques et des épicycles. Vous indiquerez en quoi l'introduction par Ptolémée du point équant constitue une "tricherie géniale" selon l'expression de Jean-Pierre Verdet.
Univers
Difficulté : ☆☆
Question 1)
Quelle est l’organisation de l’Univers chez Aristote ?
Condamnation
Difficulté : ☆☆
Question 1)
Rappeler les circonstances (scientifiques, religieuses et politiques) de la condamnation de Galilée
Nous allons utiliser le logiciel libre (opensource) Stellarium pour reproduire les observations de Galilée à padoue en 1610, à 19H.
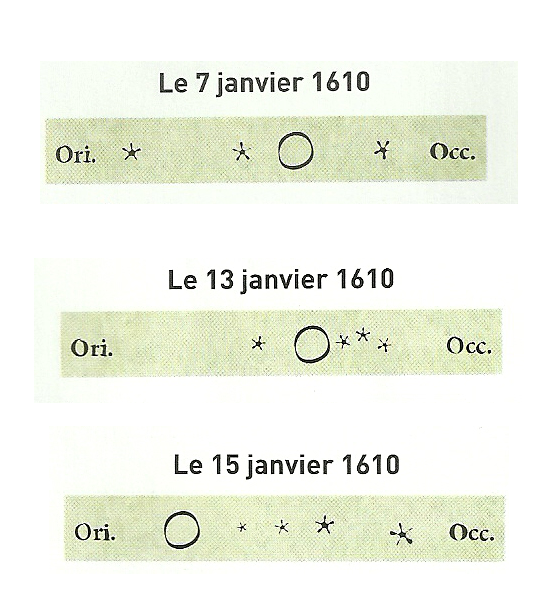
Dans son ouvrage le Sidereus Nuncius (Le Messager Céleste) publié en 1610, Galilée expose, sous la forme d’une narration accompagnée de dessins, qu’une lunette lui a permis d’observer jour après jour la planète Jupiter et son voisinage.
Crédit :
UFE / Observatoire de Paris
Stellarium est un logiciel de planétarium open source et gratuit pour votre ordinateur. Il affiche un ciel réaliste en 3D, comme si vous le regardiez à l'oeil nu, aux jumelles ou avec un télescope.
- Télécharger et installer (si ce n'est pas éjà fait) le logiciel Stellarium (bases de l'utilisation de Stellarium)
- Ouvrir Stellarium
- Choisir l'emplacement : "Padova"
- Choisir la date du 7 Janvier 1610, 19H
- Pause pour arrêter le défilement du temps
- Chercher Jupiter et centrer l'observation sur la planète
- Zoomer afin de voir les satellites de Jupiter (avec la roulette de la souris)
- Si les satellites ne se présentent pas comme sur le dessin de Galilée, inverser la monture équatoriale/azimutale (CTRL M)
- Faire défiler le temps et observer comme Galilée autour de Jupiter les 13 et d 15 janvier
Les outils de Stellarium en bas à gauche
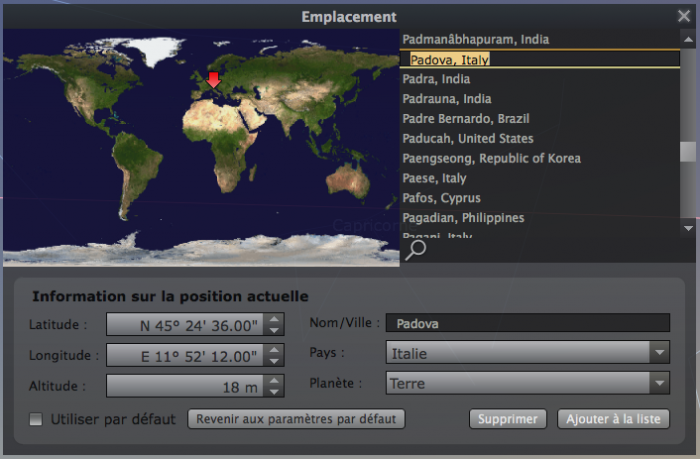
Choisir l'emplacement : "Padova
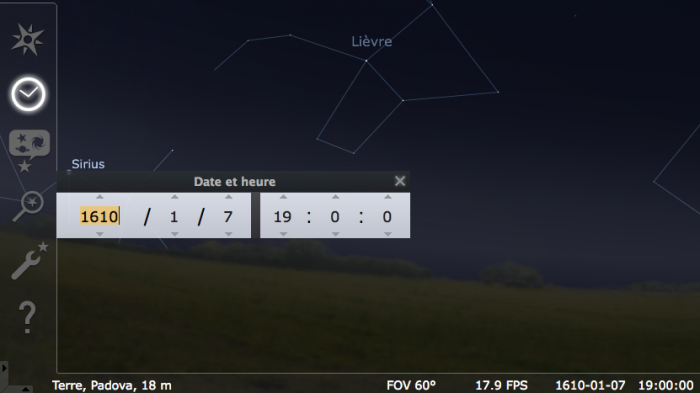
Choisir la date du 7 Janvier 1610, 19H
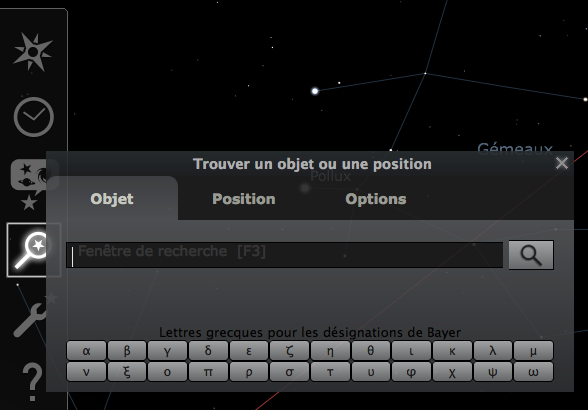
Chercher Jupiter et centrer l'observation sur la planète
Les outils de Stellarium en bas permettent d'arrêter/lancer le temps ; d'inverser la monture équatoriale/azimutale
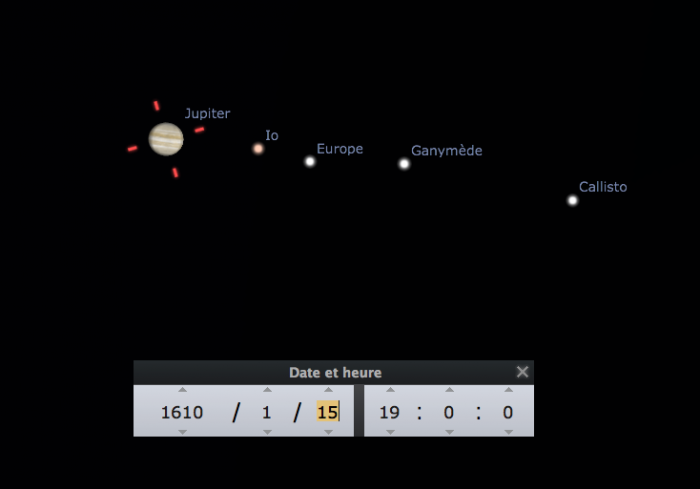
Simulation d'une observation du ciel autour de Jupiter le 15 janvier 1610
Auteur: mfl
Satellites de Jupiter
Le récit commence la nuit du 7 janvier 1610 ; l’observation est faite depuis la ville de Padoue en Italie à 19H. Il explore le ciel aux abords de la planète. Jupiter est représenté par un cercle et ses satellites par des étoiles, "Ori" indique l'est et "Occ indique l'ouest.
Les jours suivants, Galilée continue à observer cette région du ciel et il comprend que les astres qu'il a pris pour des "étoiles" tournent autour de Jupiter comme la Lune tourne autour de la Terre.
Et le 13 Janvier, pour la première fois, il aperçoit quatre astres qu'il décrit comme des "petites étoiles"…
Question 1)
Faire le croquis comme Galilée des satellites de Jupiter et de Jupiter pour les observation des 7, 13 et 15 janvier
Question 2)
Pouquoi Galilée n'a t'il représenté que trois satellites sur son dessin du 7 janvier 1610 ?
Question 3)
Décrire les trajectoires de satellites vus de la Terre
Placez-vous dans le référentiel jupitérien pour mieux comprendre les observations vues de la Terre