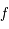 est dérivable sur
est dérivable sur ![]-\pi/2, \pi/2[](../pages_af/equations_af/equation143.png) par composition de fonction continues et dérivables.
On a:
par composition de fonction continues et dérivables.
On a:
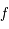 est dérivable sur
est dérivable sur ![]-\pi/2, \pi/2[](../pages_af/equations_af/equation143.png) par composition de fonction continues et dérivables.
On a:
par composition de fonction continues et dérivables.
On a:
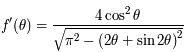 .
.
Cette fonction n'est pas définie pour 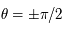 . On pose alors
. On pose alors 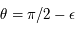 . Ainsi:
. Ainsi:
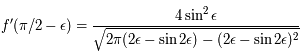 .
.
Les développements limités en zéro nous indiquent que le dénominateur est de l'ordre de 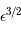 alors que le numérateur est de l'ordre de
alors que le numérateur est de l'ordre de 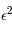 . Ainsi on a:
. Ainsi on a: 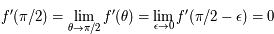 . Comme
. Comme  est impaire on a de même en prolongeant par continuité
est impaire on a de même en prolongeant par continuité 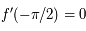 .
.