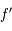 est strictement supérieur à zéro sur
est strictement supérieur à zéro sur ![]-\pi/2, \pi/2[](../pages_af/equations_af/equation159.png) , et ne s'annule qu'en
, et ne s'annule qu'en 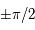 .
Ainsi
.
Ainsi 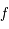 est strictement croissante sur
est strictement croissante sur 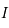 . Comme
. Comme 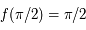 , par parité on en déduit que
, par parité on en déduit que 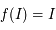 .
Donc
.
Donc 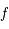 est une fonction bijective de
est une fonction bijective de 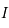 dans lui-même. Il existe donc une fonction réciproque
dans lui-même. Il existe donc une fonction réciproque 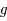 .
D'après les propriétés de
.
D'après les propriétés de 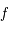 , on en déduit que
, on en déduit que 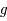 est une fonction impaire définie et continue sur
est une fonction impaire définie et continue sur 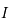 et dérivable sur
et dérivable sur 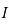 ouvert.
De plus comme on a
ouvert.
De plus comme on a ![f([0,\pi/2])=[0,\pi/2]](../pages_af/equations_af/equation172.png) , on a aussi
, on a aussi ![g([0,\pi/2])=[0,\pi/2]](../pages_af/equations_af/equation173.png) .
.