- Si
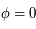 , alors l'équation (*) admet
, alors l'équation (*) admet 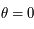 comme solution (en effet
comme solution (en effet 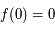 , c'est-à-dire
, c'est-à-dire 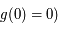 . Ainsi
. Ainsi 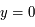 et
et 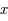 varie de
varie de 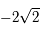 à
à 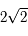 lorsque
lorsque 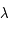 varie de
varie de 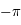 à
à 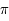 .
.
- Pour le pôle nord, on a
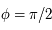 . Or
. Or 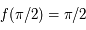 , soit
, soit 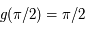 , ainsi
, ainsi 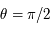 . L'image du pôle nord est
. L'image du pôle nord est 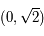 .
Par symétrie, le pôle Sud a pour image
.
Par symétrie, le pôle Sud a pour image 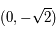 .
.
- Dans ce cas on a
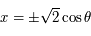 et
et 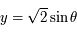 (le signe "+" correspond à la longitude positive). Les points se trouvent donc sur un demi-cercle centré à l'origine et de rayon
(le signe "+" correspond à la longitude positive). Les points se trouvent donc sur un demi-cercle centré à l'origine et de rayon 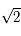 se trouvant à droite de l'axe des ordonnées pour la longitude positive et à gauche pour la longitude négative. Comme un méridien correspond à l'ensemble des latitudes
se trouvant à droite de l'axe des ordonnées pour la longitude positive et à gauche pour la longitude négative. Comme un méridien correspond à l'ensemble des latitudes ![\phi \in [-\pi/2,\pi/2]](../pages_af/equations_af/equation199.png) , chaque demi-cercle est décrit complètement d'après la propriété de la fonction
, chaque demi-cercle est décrit complètement d'après la propriété de la fonction 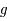 :
: ![g([-\pi/2,\pi/2])=[-\pi/2,\pi/2]](../pages_af/equations_af/equation201.png) .
.
- Dans ce cas on a
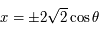 et
et 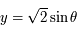 . Comme à la question précédente sauf que les points se trouvent sur deux demi-ellipses d'une ellipse centrée à l'origine et de demi-petit axe
. Comme à la question précédente sauf que les points se trouvent sur deux demi-ellipses d'une ellipse centrée à l'origine et de demi-petit axe 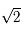 parallèle à l'axe des ordonnées et de demi-grand axe
parallèle à l'axe des ordonnées et de demi-grand axe 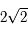 . Toute l'ellipse est décrite, pour la même raison que précédemment.
. Toute l'ellipse est décrite, pour la même raison que précédemment.
- Si on note
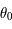 la solution de l'équation (*) pour la latitude
la solution de l'équation (*) pour la latitude 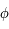 , i.e.
, i.e. 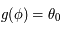 , alors
, alors 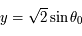 et
et 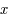 varie de
varie de 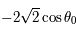 à
à 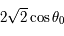 lorsque
lorsque 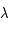 varie de
varie de 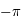 à
à 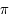 . C'est une corde de l'ellipse parallèle à l'axe des abcisses.
. C'est une corde de l'ellipse parallèle à l'axe des abcisses.
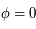 , alors l'équation (*) admet
, alors l'équation (*) admet 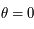 comme solution (en effet
comme solution (en effet 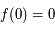 , c'est-à-dire
, c'est-à-dire 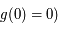 . Ainsi
. Ainsi 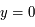 et
et 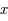 varie de
varie de 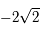 à
à 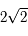 lorsque
lorsque 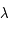 varie de
varie de 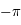 à
à 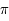 .
. 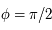 . Or
. Or 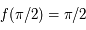 , soit
, soit 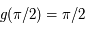 , ainsi
, ainsi 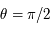 . L'image du pôle nord est
. L'image du pôle nord est 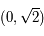 .
Par symétrie, le pôle Sud a pour image
.
Par symétrie, le pôle Sud a pour image 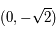 .
. 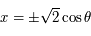 et
et 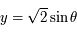 (le signe "+" correspond à la longitude positive). Les points se trouvent donc sur un demi-cercle centré à l'origine et de rayon
(le signe "+" correspond à la longitude positive). Les points se trouvent donc sur un demi-cercle centré à l'origine et de rayon 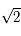 se trouvant à droite de l'axe des ordonnées pour la longitude positive et à gauche pour la longitude négative. Comme un méridien correspond à l'ensemble des latitudes
se trouvant à droite de l'axe des ordonnées pour la longitude positive et à gauche pour la longitude négative. Comme un méridien correspond à l'ensemble des latitudes ![\phi \in [-\pi/2,\pi/2]](../pages_af/equations_af/equation199.png) , chaque demi-cercle est décrit complètement d'après la propriété de la fonction
, chaque demi-cercle est décrit complètement d'après la propriété de la fonction 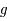 :
: ![g([-\pi/2,\pi/2])=[-\pi/2,\pi/2]](../pages_af/equations_af/equation201.png) .
.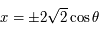 et
et 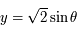 . Comme à la question précédente sauf que les points se trouvent sur deux demi-ellipses d'une ellipse centrée à l'origine et de demi-petit axe
. Comme à la question précédente sauf que les points se trouvent sur deux demi-ellipses d'une ellipse centrée à l'origine et de demi-petit axe 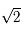 parallèle à l'axe des ordonnées et de demi-grand axe
parallèle à l'axe des ordonnées et de demi-grand axe 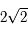 . Toute l'ellipse est décrite, pour la même raison que précédemment.
. Toute l'ellipse est décrite, pour la même raison que précédemment. 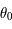 la solution de l'équation (*) pour la latitude
la solution de l'équation (*) pour la latitude 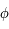 , i.e.
, i.e. 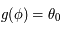 , alors
, alors 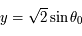 et
et 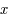 varie de
varie de 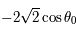 à
à 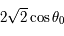 lorsque
lorsque 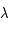 varie de
varie de 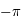 à
à 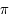 . C'est une corde de l'ellipse parallèle à l'axe des abcisses.
. C'est une corde de l'ellipse parallèle à l'axe des abcisses.