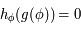 , or
, or 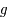 est impaire, donc
est impaire, donc 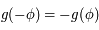 , ce qui répond au premier point. Ensuite, comme
, ce qui répond au premier point. Ensuite, comme ![g([0,\pi/2])=[0,\pi/2]](../pages_af/equations_af/equation232.png) on en déduit que si
on en déduit que si ![\phi\in[0,\pi/2]](../pages_af/equations_af/equation233.png) alors la solution de
alors la solution de 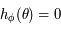 est dans
est dans ![[0,\pi/2]](../pages_af/equations_af/equation235.png) . Les deux dernières égalités viennent directement du fait que
. Les deux dernières égalités viennent directement du fait que 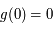 et
et 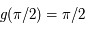 .
.
On a 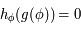 , or
, or 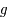 est impaire, donc
est impaire, donc 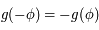 , ce qui répond au premier point. Ensuite, comme
, ce qui répond au premier point. Ensuite, comme ![g([0,\pi/2])=[0,\pi/2]](../pages_af/equations_af/equation232.png) on en déduit que si
on en déduit que si ![\phi\in[0,\pi/2]](../pages_af/equations_af/equation233.png) alors la solution de
alors la solution de 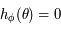 est dans
est dans ![[0,\pi/2]](../pages_af/equations_af/equation235.png) . Les deux dernières égalités viennent directement du fait que
. Les deux dernières égalités viennent directement du fait que 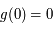 et
et 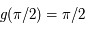 .
.