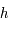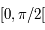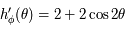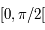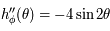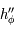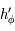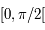h est définie continue dérivable sur [0,\pi/2[ comme composée de fonctions définies continues et dérivables. On a h_\phi'(\theta)=2+2\cos 2\theta qui est continue et strictement positive sur [0,\pi/2[. Elle est aussi dérivable, avec h_\phi'' (\theta)=-4\sin 2\theta. h_\phi'' est strictement négative sur ]0,\pi/2[ et nulle en 0. Ainsi h_\phi' est strictement décroissante sur [0,\pi/2[.