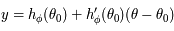L'équation de la tangente est . Pour 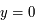on obtient 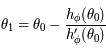. Comm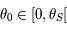e , que 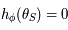et que 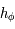est croissante, on en déduit que 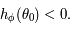De plus 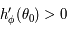ainsi on a bien 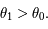D'après le théorème des accroissements finis, il existe tel que 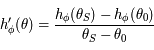. Ainsi, en considérant 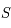comme le point d'intersection entre l'axe des abscisses et la droite passant par 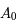et de coefficient directeur 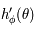, on a 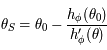. Comme 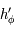est une fonction strictement décroissante sur , on en déduit que 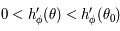, soit 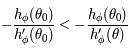. Ainsi on a bien 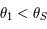.