![\phi\in]0,\pi/2[](../pages_af/equations_af/equation300.png) alors
alors ![\theta_S\in]0,\pi/2[](../pages_af/equations_af/equation301.png) . Autrement dit
. Autrement dit 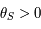 , donc
, donc 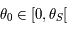 . Ainsi d'après la question précédente on sait que
. Ainsi d'après la question précédente on sait que 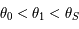 . Donc
. Donc 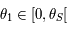 .
Si on suppose maintenant
.
Si on suppose maintenant 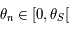 alors, toujours d'après la question précédente on a
alors, toujours d'après la question précédente on a 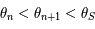 , en outre
, en outre 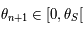 .
Ainsi,
.
Ainsi, 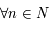 on a
on a 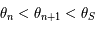 . Donc la suite
. Donc la suite 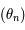 est croissante et majorée, donc elle converge vers une limite
est croissante et majorée, donc elle converge vers une limite 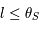 .
Par continuité de
.
Par continuité de 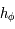 et
et 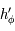 , on a
, on a 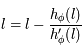 , et comme
, et comme 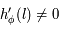 , on en déduit que
, on en déduit que 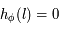 , donc
, donc 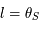 .
.