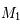 à l'origine et
à l'origine et 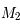 qui nous définie l'axe des abscisses ainsi que la norme. Ainsi on a
qui nous définie l'axe des abscisses ainsi que la norme. Ainsi on a 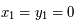 , et
, et 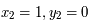 .
.
Comme on est libre sur le système de coordonnées, on peut choisir 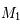 à l'origine et
à l'origine et 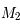 qui nous définie l'axe des abscisses ainsi que la norme. Ainsi on a
qui nous définie l'axe des abscisses ainsi que la norme. Ainsi on a 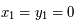 , et
, et 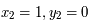 .
.
Le système devient :
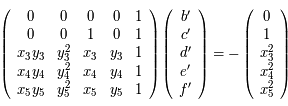 .
.
Qu'on peut écrire :
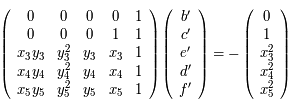 .
.
Ainsi  et
et 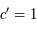 .
.
Le système à résoudre est donc :
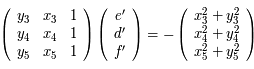 .
.