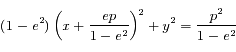SOLUTION

L'équation de la conique peut s'écrire : 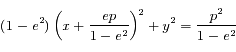$(1-e^2)\left(x+\frac{ep}{1-e^2}\right)^2+y^2=\frac{p^2}{1-e^2}$ qui devient :

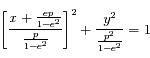
$\left\lbrack\frac{x+\frac{ep}{1-e^2}}{\frac{p}{1-e^2}}\right\rbrack^2+\frac{y^2}{\frac{p^2}{1-e^2}}=1$

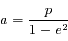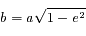En posant $a=\frac{p}{1-e^2}$ et $b=a\sqrt{1-e^2}$ (qui est défini puisque 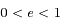0<e<1 ), l'équation devient:

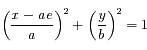
$\left(\frac{x-ae}{a}\right)^2+\left(\frac{y}{b}\right)^2=1$

qui est l'équation d'une ellipse dont le centre a pour coordonnées 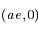(ae,0) , de demi-grand axe 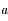et de demi-petit axe .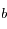