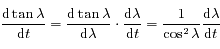SOLUTION

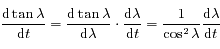On a: $\frac{{\rm d} \tan \lambda}{{\rm d}t}=\frac{{\rm d} \tan \lambda}{{\rm d}\lambda}\cdot \frac{{\rm d} \lambda}{{\rm d}t}=\frac{1}{\cos^2 \lambda} \frac{{\rm d} \lambda}{{\rm d}t}$ .

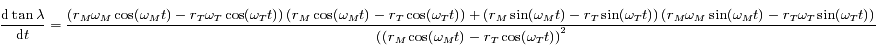
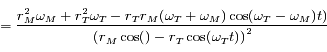Or $\frac{{\rm d} \tan \lambda}{{\rm d}t}=\frac{\left(r_M \omega_M \cos (\omega_Mt)-r_T\omega_T\cos (\omega_Tt)\right)\left(r_M\cos (\omega_M t)-r_T\cos (\omega_T t)\right) + \left(r_M\sin (\omega_M t)-r_T\sin (\omega_T t)\right)\left(r_M \omega_M \sin (\omega_Mt)-r_T\omega_T\sin (\omega_Tt)\right)}{\left((r_M\cos (\omega_M t)-r_T\cos (\omega_T t)\right)^2}$ $=\frac{r_M^2\omega_M+r_T^2\omega_T-r_Tr_M(\omega_T+\omega_M)\cos(\omega_T-\omega_M)t)}{\left(r_M\cos(\omegat)-r_T\cos(\omega_Tt)\right)^2}$ .

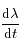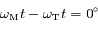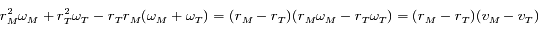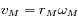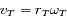Le signe de $\frac{{\rm d} \lambda}{{\rm d} t}$ est celui du numérateur de l'expression ci-dessus. Ainsi, quand $\omega_{\rm M}t-\omega_{\rm T}t=0^\circ$ , le signe de la dérivée est celui de $r_M^2\omega_M+r_T^2\omega_T-r_Tr_M(\omega_M+\omega_T)=(r_M-r_T)(r_M\omega_M-r_T\omega_T)=(r_M-r_T)(v_M-v_T)$ , oùt $v_M=r_M\omega_M$ et $v_T=r_T\omega_T$ .

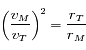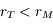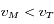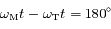Or d'après la propriété dérivant de la troisième loi de Kepler, on a $\left(\frac{v_M}{v_T}\right)^2=\frac{r_T}{r_M}$ . Ainsi, pour Mars on a r_T<r_M et v_M<v_T , donc la dérivée est négative. De même on montre que pour $\omega_{\rm M}t-\omega_{\rm T}t=180^\circ$ , la dérivée est positive.

On en conclue qu'effectivement lors de l'opposition ( 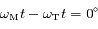$\omega_{\rm M}t-\omega_{\rm T}t=0^\circ$ ), le mouvement de Mars est rétrograde, alors qu'à la conjonction 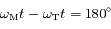$\omega_{\rm M}t-\omega_{\rm T}t=180^\circ$ , le mouvement est prograde.