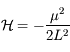SOLUTION

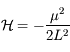On a $\mathcal H=-\frac{\mu^2}{2L^2}$ , ainsi les équations de hamilton nous donnent:

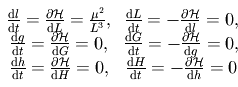$\large \begin{array}{cc}\frac{\mathrm d l}{\mathrm d t}=\frac{\partial \mathcal H}{\mathrm d L}=\frac{\mu^2}{L^3}, & \frac{\mathrm d L}{\mathrm d t}=-\frac{\partial \mathcal H}{\mathrm d l}=0,\\ \frac{\mathrm d g}{\mathrm d t}=\frac{\partial \mathcal H}{\mathrm d G}=0, & \frac{\mathrm d G}{\mathrm d t}=-\frac{\partial \mathcal H}{\mathrm d g}=0, \\ \frac{\mathrm d h}{\mathrm d t}=\frac{\partial \mathcal H}{\mathrm d H}=0, & \frac{\mathrm d H}{\mathrm d t}=-\frac{\partial \mathcal H}{\mathrm d h}=0 \end{array}$ .

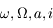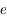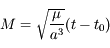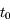Ainsi, $\omega, \Omega, a, i$ et sont constants. Seule l'anomalie moyenne varie, et est donnée par $M=\sqrt{\frac{\mu}{a^3}}(t-t_0)$ , où t_0 correspond au passage au péricentre, c'est à dire lorsque 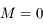M=0 . Avec 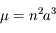$\mu=n^2a^3$ on retrouve bien la définition 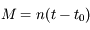M=n(t-t_0) de l'anomalie moyenne donnée dans l'exercice sur l'équation de Kepler.