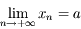 . Donc d'après la définition de
. Donc d'après la définition de 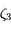 , on a aussi
, on a aussi 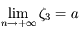 . Comme
. Comme 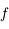 est de classe
est de classe 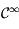 sur
sur 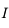 , sa dérivée première est continue, donc
, sa dérivée première est continue, donc 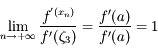 . Dautre part on a
. Dautre part on a 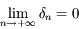 donc, d'après l'expression obtenue précedemment pour
donc, d'après l'expression obtenue précedemment pour 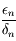 , on a bien la limite demandée.
, on a bien la limite demandée.
On sait par hypothèse que 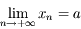 . Donc d'après la définition de
. Donc d'après la définition de 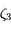 , on a aussi
, on a aussi 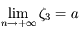 . Comme
. Comme 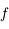 est de classe
est de classe 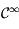 sur
sur 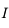 , sa dérivée première est continue, donc
, sa dérivée première est continue, donc 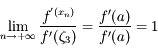 . Dautre part on a
. Dautre part on a 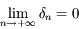 donc, d'après l'expression obtenue précedemment pour
donc, d'après l'expression obtenue précedemment pour 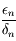 , on a bien la limite demandée.
, on a bien la limite demandée.