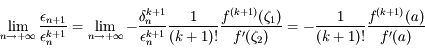SOLUTION

On a:

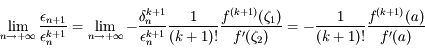$\lim_{n\to +\infty}\frac{\epsilon_{n+1}}{\epsilon_n^{k+1}}=\lim_{n\to +\infty} -\frac{\delta_{n}^{k+1}}{\epsilon_n^{k+1}}\frac{1}{(k+1)!}\frac{f^{(k+1)}(\zeta_1)}{f'(\zeta_2)}=-\frac{1}{(k+1)!}\frac{f^{(k+1)}(a)}{f'(a)}$ .

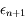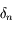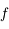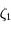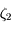La première égalité vient de l'expression de $\epsilon_{n+1}$ en fonction de $\delta_{n}$ calculée prcédemment et la deuxième découle de la continuité des dérivées successives de et de la définition de $\zeta_1$ et $\zeta_2$ .

La conlusion découle de la définition de la convergence à l'ordre 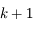k+1 .