SOLUTION

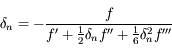
On a:

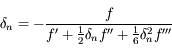
$\delta_n=-\frac{f}{f'+\frac{1}{2}\delta_nf''+\frac{1}{6}\delta_n^2f'''}$

où on a omis la variable 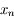x_n pour simplifier.

En utilisant le dévelopement limité de 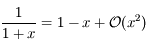$\frac{1}{1+x}=1-x+\mathcal{O}(x^2)$ , on a:

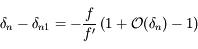$\delta_n-\delta_{n1}=-\frac{f}{f'}\left( 1+\mathcal{O}(\delta_n)-1\right)$ .

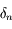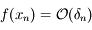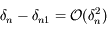Or, d'après la définition de $\delta_n$ : $f(x_n)=\mathcal{O}(\delta_n)$ , donc $\delta_n-\delta_{n1}=\mathcal{O}(\delta_n^2)$ .

De même:

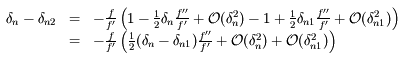$\begin{array}{rcl}\delta_n-\delta_{n2}&=&-\frac{f}{f'}\left(1-\frac{1}{2}\delta_n\frac{f''}{f'}+\mathcal{O}(\delta_n^2)-1+\frac{1}{2}\delta_{n1}\frac{f''}{f'}+\mathcal{O}(\delta_{n1}^2)\right)\\ &=&-\frac{f}{f'}\left(\frac{1}{2}(\delta_n-\delta_{n1})\frac{f''}{f'}+\mathcal{O}(\delta_n^2)+\mathcal{O}(\delta_{n1}^2)\right)\end{array}$ ,

qui, d'après le résultat précédent nous donne 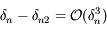$\delta_n-\delta_{n2}=\mathcal{O}(\delta_n^3)$ .

Enfin, on a:

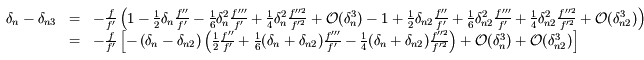$\begin{array}{rcl}\delta_n-\delta_{n3}&=&-\frac{f}{f'}\left(1-\frac{1}{2}\delta_n\frac{f''}{f'}-\frac{1}{6}\delta_n^2\frac{f'''}{f'}+\frac{1}{4}\delta_n^2\frac{f''^2}{f'^2}+\mathcal{O}(\delta_n^3)-1+\frac{1}{2}\delta_{n2}\frac{f''}{f'}+\frac{1}{6}\delta_{n2}^2\frac{f'''}{f'}+\frac{1}{4}\delta_{n2}^2\frac{f''^2}{f'^2}+\mathcal{O}(\delta_{n2}^3)\right)\\ &=&-\frac{f}{f'}\left\lbrack-\left(\delta_n-\delta_{n2}\right)\left(\frac{1}{2}\frac{f''}{f'}+\frac{1}{6}(\delta_n+\delta_{n2})\frac{f'''}{f'}-\frac{1}{4}(\delta_n+\delta_{n2})\frac{f''^2}{f'^2}\right)+\mathcal{O}(\delta_n^3)+\mathcal{O}(\delta_{n2}^3)\right\rbrack\end{array}$ ,

En utilisant les résutlats précédents, on trouve bien: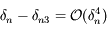 $\delta_n-\delta_{n3}=\mathcal{O}(\delta_n^4)$ .