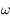 est constant, on a
est constant, on a 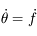 . Ainsi
. Ainsi 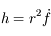 . La solution des équations du mouvement peut aussi s'écrire:
. La solution des équations du mouvement peut aussi s'écrire:
Comme 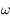 est constant, on a
est constant, on a 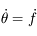 . Ainsi
. Ainsi 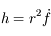 . La solution des équations du mouvement peut aussi s'écrire:
. La solution des équations du mouvement peut aussi s'écrire:
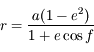 ,
,
Ainsi:
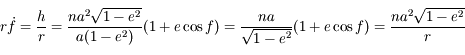 .
.
De même en différentiant l'équation précédente obtenue pour 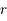 on obtient:
on obtient:
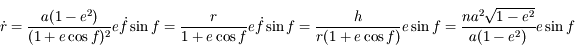 .
.
Ce qui correspond bien à l'équation demandée.