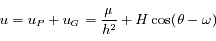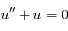 . Le polynôme caractéristique de l'équation est
. Le polynôme caractéristique de l'équation est 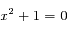 , qui a deux solutions complexes conjuguées
, qui a deux solutions complexes conjuguées  et
et 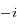 (où
(où  est tel que
est tel que 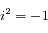 ). Ainsi la solution générale de l'équation sans second membre s'écrit:
). Ainsi la solution générale de l'équation sans second membre s'écrit:
C'est une équation linéaire du second ordre avec second membre et à coefficients constants.
On commence par résoudre l'équation sans second membre: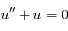 . Le polynôme caractéristique de l'équation est
. Le polynôme caractéristique de l'équation est 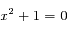 , qui a deux solutions complexes conjuguées
, qui a deux solutions complexes conjuguées  et
et 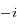 (où
(où  est tel que
est tel que 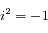 ). Ainsi la solution générale de l'équation sans second membre s'écrit:
). Ainsi la solution générale de l'équation sans second membre s'écrit:
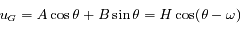
où 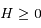 et
et 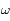 sont des constantes du mouvement dépendant des conditions initiales.
sont des constantes du mouvement dépendant des conditions initiales.
Une solution particulière de l'équation est 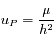 .
On en déduit la solution générale de notre équation:
.
On en déduit la solution générale de notre équation: