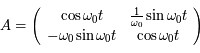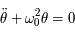
L'équation différentielle (du second ordre) à considérer est:
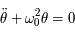
La solution générale est donc
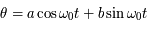
et donc:
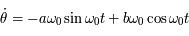
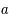 et
et 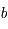 sont des constantes arbitraires que l'on va déterminer pour chacun des vecteur de la base canonique.
sont des constantes arbitraires que l'on va déterminer pour chacun des vecteur de la base canonique.
La première colonne de 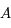 correspond à la solution de condition initiale
correspond à la solution de condition initiale 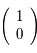 dans la notation matricielle:
dans la notation matricielle:
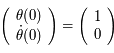
Ce qui donne 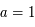 et
et 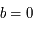 . Soit
. Soit 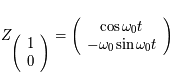
La deuxième colonne de 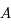 correspond à la solution de condition initiale
correspond à la solution de condition initiale 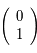 dans la notation matricielle:
dans la notation matricielle:
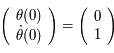
Ce qui donne 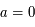 et
et 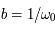 . Soit
. Soit 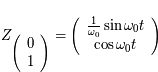
Ainsi