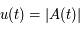 . On a:
. On a:
On pose encore 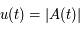 . On a:
. On a:
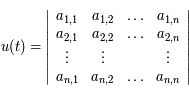
Par la forme mutilinéaire du déterminant, on 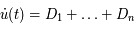 , avec
, avec
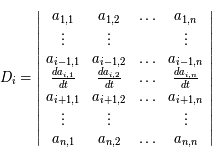
On "développe" 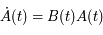 , soit:
, soit:
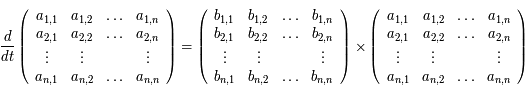
Ainsi la ligne 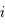 de
de 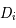 est :
est :
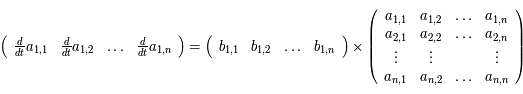
Cette ligne est donc une combinaison linéaire des lignes de 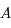 . Or dans un déterminant, on peut remplacer une ligne par cette même ligne à laquelle on ajoute une combinaison linéaire des autres lignes. On a ainsi:
. Or dans un déterminant, on peut remplacer une ligne par cette même ligne à laquelle on ajoute une combinaison linéaire des autres lignes. On a ainsi:
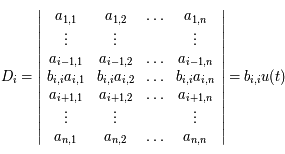
Ainsi, on a bien : 