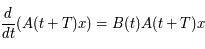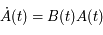 par
par 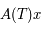 , on obtient
, on obtient
En multipliant à droite chaque membre de la relation 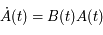 par
par 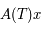 , on obtient
, on obtient
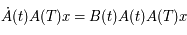
Donc 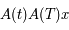 est solution de l'équation de Mathieu (sous forme matricielle:
est solution de l'équation de Mathieu (sous forme matricielle: 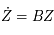 ) de condition initiale
) de condition initiale 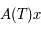 .
.
Il reste à montrer que 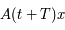 est solution aussi (avec la même condition initiale
est solution aussi (avec la même condition initiale 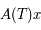 ).
).
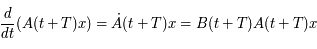
car 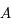 est solution de
est solution de 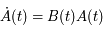 . De plus la matrice
. De plus la matrice 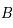 est périodique de période
est périodique de période 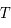 . On a finalement:
. On a finalement: