Auteur: Alain Vienne
 Magnitude du Soleil vu de alpha du Centaure
Magnitude du Soleil vu de alpha du Centaure
Difficulté : ☆
Temps : 30mn
Question 1)
Vu de la Terre, le Soleil a une magnitude apparente égale à -27. Calculer la magnitude apparente qu'aurait le Soleil s'il était observé depuis l'étoile alpha du Centaure. La parallaxe de cette étoile est 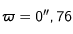 .
.
La parallaxe d'une étoile est l'angle sous lequel on voit le rayon de l'orbite de la Terre depuis cette étoile. D'après la définition du parsec, on en déduit immédiatement que 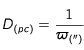 . Cette relation n'est valable que dans les unités indiquées.
. Cette relation n'est valable que dans les unités indiquées.
Auteur: Alain Vienne
 Magnitudes absolues du Soleil et de Véga
Magnitudes absolues du Soleil et de Véga
Difficulté : ☆
Temps : 20mn
Question 1)
Calculer la magnitude absolue du Soleil et celle de Véga (dont la parallaxe est 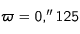 )
)
Auteur: Alain Vienne
 Magnitude de l'amas des pleïades
Magnitude de l'amas des pleïades
Difficulté : ☆
Temps : 30mn
Question 1)
L'amas des pléiades contient 7 étoiles visibles à l'oeil nu:
| Etoile |
magnitude |
| Alcyone |
3,00 |
| Atlas |
3,80 |
| Electra |
3,80 |
| Maia |
4,00 |
| Merope |
4,30 |
| Taggeta |
4,40 |
| Pleione |
5,00 |
Calculer la magnitude globale de l'amas.
Ce ne peut être la somme des magnitudes (!) puisque l'échelle est logarithmique.
Auteur: Alain Vienne
 Visibilités des satellites de mars
Visibilités des satellites de mars
Difficulté : ☆
Temps : 20mn
Question 1)
A partir de quelle distance à la planète Mars, un voyageur vers cette planète pourra-t-il voir à l'oeil nu les satellites de Mars? On donne les magnitudes de Phobos et Deimos vus de la Terre à l'opposition de Mars: 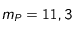 et
et 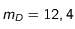 . On supposera que l'orbite de Mars est un cercle de rayon 1,524 UA.
. On supposera que l'orbite de Mars est un cercle de rayon 1,524 UA.
Dire que Mars est vu à l'oppostion signifie que Mars est du côté opposé au Soleil vu de la Terre.
Auteur: Alain Vienne
 Magnitude apparente d'une planète
Magnitude apparente d'une planète
Difficulté : ☆☆
Temps : 50mn
Question 2)
Application à Jupiter pour lequel 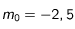 et
et 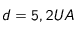 , puis à Mars pour lequel
, puis à Mars pour lequel 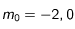 et
et 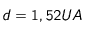 : Calculer la magnitude de ces planètes lorsqu'elles sont en quadrature.
: Calculer la magnitude de ces planètes lorsqu'elles sont en quadrature.
A la quadrature, on peut appliquer le théorême de Pythagore.
Auteur: Alain Vienne
 Magnitude instrumentale
Magnitude instrumentale
Difficulté : ☆☆
Temps : 60mn
Question 1)
On observe à l'oeil nu une étoile de magnitude apparente 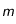 . On l'observe ensuite au travers d'un instrument dont le diamètre d'ouverture est
. On l'observe ensuite au travers d'un instrument dont le diamètre d'ouverture est 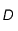 avec une pupille de sortie dont le diamètre
avec une pupille de sortie dont le diamètre 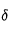 est égal à celle de l'oeil.
est égal à celle de l'oeil.
Quelle est la magnitude instrumentale 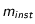 de cette étoile au travers de cet instrument.
de cette étoile au travers de cet instrument.
Question 2)
Quelle est la magnitude limite observable avec cet instrument?
Question 3)
Faire l'application numérique avec les télescopes d'ouverture suivante: 5cm, 20cm, 1m, 8 m. On prendra 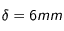
Auteur: Stéphane Erard
Les éléments chimiques les plus légers sont formés au début de l'univers, les plus lourds sont formés essentiellement dans les étoiles.
Tous ne sont pas stables. Un radionucléide est un noyau atomique instable qui se désintègre en une autre espèce. La probabilité de désintégration de chaque atome est constante au cours du temps, et les événements sont indépendants.
Auteur: Stéphane Erard
 Désintégration radioactive
Désintégration radioactive
Difficulté : ☆
Temps : 15 min
Question 1)
On considère une seule espèce radioactive. Soit N(t) le nombre d'atomes à l'instant t, quel est le nombre de désintégrations dN pendant l'intervalle de temps dt ?
Rappel : le nombre de désintégrations est par hypothèse proportionnel à la quantité d'atomes de l'espèce considérée.
Question 2)
En déduire le nombre d'atomes présents à l'instant t.
On appelle 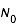 le nombre d'atomes au temps 0.
le nombre d'atomes au temps 0.
Question 3)
Au bout de quel intervalle de temps 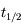 le nombre d'atomes radioactifs est-il réduit de moitié ?
le nombre d'atomes radioactifs est-il réduit de moitié ?
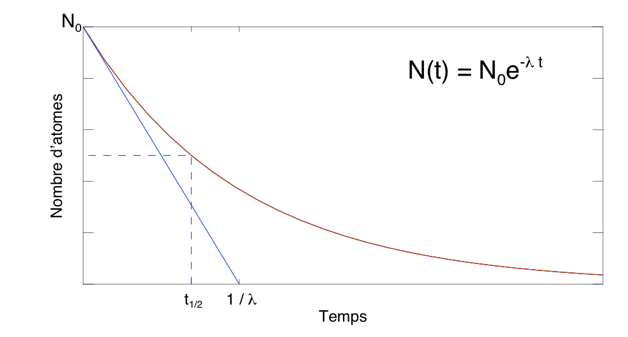
Tracer la courbe d'évolution et sa tangente à l'instant initial. Reporter 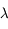 et
et 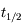 .
.
Question 4)
On définit l'activité A comme le nombre de désintégrations par seconde d'une espèce. C'est une grandeur observable, qui se mesure en Becquerels (Bq) dans le Système International. Exprimer celle-ci en fonction du temps.
Auteur: Stéphane Erard
 Datation de météorites
Datation de météorites
Difficulté : ☆
Temps : 30 min
On utilise la loi de décroissance radioactive pour dater un échantillon de météorite. Les âges étant élevés (de l'ordre de l'âge du Système solaire, ~5 milliards d'années) on utilise des isotopes à longue période.
Le rubidium 87 décroît par radioactivité 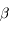 en strontium 87 avec une demi-vie de 49 milliards d'années, selon la réaction suivante :
en strontium 87 avec une demi-vie de 49 milliards d'années, selon la réaction suivante :
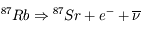
Un des neutrons se transforme en proton (radioactivité 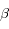 ). Le nombre de masse (87) est inchangé, le nombre de charges varie (de 37 à 38). La charge totale est conservée par l'émission d'un électron. La quatrième particule est un anti-neutrino symétrique de l'électron, dont la présence est requise par la conservation du moment cinétique.
). Le nombre de masse (87) est inchangé, le nombre de charges varie (de 37 à 38). La charge totale est conservée par l'émission d'un électron. La quatrième particule est un anti-neutrino symétrique de l'électron, dont la présence est requise par la conservation du moment cinétique.
Question 1)
Ecrire la quantité de 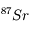 à l'instant de la mesure t en fonction des quantités de
à l'instant de la mesure t en fonction des quantités de 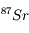 initiale et de
initiale et de 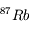 actuelle et initiale.
actuelle et initiale.
Question 2)
Récrire cette équation pour éliminer une des quantités inconnues.
En pratique, on mesure des rapports d'abondance ; en l'occurrence on rapporte toutes les abondances à celle du 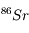 , isotope stable du strontium qui n'est pas un produit de désintégration (son abondance n'est donc pas fonction du temps). Faire apparaître ces rapports. Commentaires ?
, isotope stable du strontium qui n'est pas un produit de désintégration (son abondance n'est donc pas fonction du temps). Faire apparaître ces rapports. Commentaires ?
Question 3)
On lève l'indétermination précédente en effectuant cette mesure sur différents minéraux présents dans la même météorite, et formés au même moment. Reporter les points de mesures attendus sur un graphique dérivé de la fonction précédente.
L'équation est celle d'une simple droite, dont la pente change au cours du temps.
Question 4)
Les mesures des rapports isotopiques dans l'exemple sont les suivantes :
Rapports isotopiques
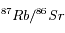
|
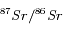
|
| 0.059 |
0.703 |
| 0.137 |
0.708 |
| 0.158 |
0.709 |
| 0.295 |
0.718 |
| 0.323 |
0.720 |
| 0.376 |
0.724 |
| 0.386 |
0.724 |
Trouver un ordre de grandeur de l'âge de la météorite à l'aide des chiffres fournis. Que mesure-t-on exactement avec cette méthode ?
On calcule la droite de régression en appliquant le modèle linéaire ci-dessus. On en déduit :
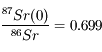
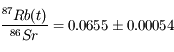
-
Question 1
Solution :
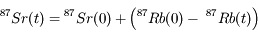
-
Question 2
Solution :
![\frac{^{87}Sr(t)}{^{86}Sr} = \frac{^{87}Sr(0)}{^{86}Sr} + \frac{^{87}Rb(t)}{^{86}Sr} + \left[ exp(\lambda t) -1 \right]](../pages_exp/equations_exp/equation77.png)
On n'a qu'une équation pour quatre quantités dont seulement deux sont mesurables. Il nous manque pour conclure la quantité initiale de strontium (ou son rapport isotopique initial).
-
Question 3
Aide :
L'équation est celle d'une simple droite, dont la pente change au cours du temps.
Solution :
isochrones
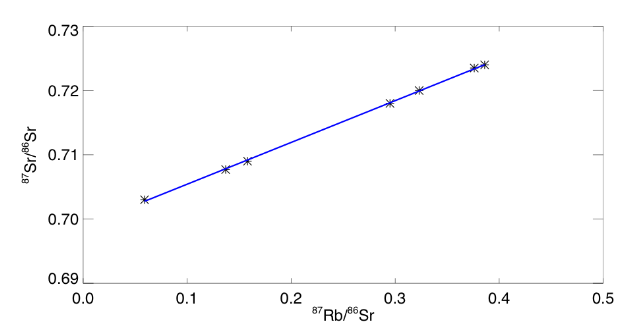
Mesures des minéraux de la chondrite ordinaire de Tieschitz et datation par la méthode rubidium/strontium (mesures de Wasserburg et al.).
Les différents minéraux contiennent a priori des quantités différentes de Rb et Sr, mais les points sont alignés sur une droite. La pente de cette droite varie au cours du temps, d'où son nom d'isochrone. L'ordonnée à l'origine est le rapport isotopique initial du Sr.
-
Question 4
Aide :
On calcule la droite de régression en appliquant le modèle linéaire ci-dessus. On en déduit :
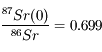
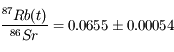
Solution :
L'âge estimé est de 4,45 ± 0.04 milliards d'années. Il s'agit d'un des matériaux les plus anciens du Système solaire.
On mesure de cette façon le temps écoulé depuis le moment où les éléments considérés sont piégés dans la roche, et coupés d'autres sources de Rb et Sr — c'est en l'occurrence le moment de la cristallisation. D'autres couples de radionucléides permettent de sonder d'autres échelles de temps, ou des événements plus récents dans l'histoire de la roche (activité volcanique tardive, dégazage, temps passé dans le milieu interplanétaire…).
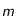 :
: 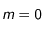 pour l'étoile la plus brillante du ciel (Véga de la constellation de la Lyre) et
pour l'étoile la plus brillante du ciel (Véga de la constellation de la Lyre) et 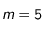 est souvent considéré comme la limite des étoiles visibles à l'oeil nu. Avec les plus grands télescopes actuels, on peut voir jusqu'à la magnitude 30. A l'inverse, le Soleil qui est très "éclatant" a une magnitude -27.
est souvent considéré comme la limite des étoiles visibles à l'oeil nu. Avec les plus grands télescopes actuels, on peut voir jusqu'à la magnitude 30. A l'inverse, le Soleil qui est très "éclatant" a une magnitude -27.
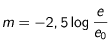 où
où 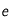 est l'éclat de l'astre que l'on observe.
est l'éclat de l'astre que l'on observe. 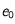 est l'éclat de l'étoile Véga qui est ainsi prise en référence (pour assurer que sa magnitude apparente est 0). On rappelle que la notation
est l'éclat de l'étoile Véga qui est ainsi prise en référence (pour assurer que sa magnitude apparente est 0). On rappelle que la notation 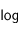 désigne le logarithme en base 10.
désigne le logarithme en base 10.
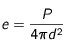 où
où 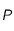 est la puissance totale émise par l'astre et
est la puissance totale émise par l'astre et 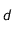 est sa distance.
est sa distance.
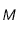 . C'est la magnitude qu'aurait cet astre si il était observé à la distance de 10 parsecs. On a donc pour un même astre :
. C'est la magnitude qu'aurait cet astre si il était observé à la distance de 10 parsecs. On a donc pour un même astre :  et
et  avec
avec 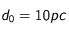
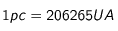 (de la même manière qu'il y a 206265 " dans un radian).
(de la même manière qu'il y a 206265 " dans un radian).
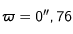 .
.
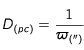 . Cette relation n'est valable que dans les unités indiquées.
. Cette relation n'est valable que dans les unités indiquées.
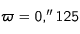 )
)
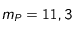 et
et 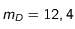 . On supposera que l'orbite de Mars est un cercle de rayon 1,524 UA.
. On supposera que l'orbite de Mars est un cercle de rayon 1,524 UA.
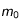 . Exprimez la magnitude de cette planète lorsqu'elle est à la distance
. Exprimez la magnitude de cette planète lorsqu'elle est à la distance  de la Terre et à la distance
de la Terre et à la distance 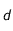 du Soleil. On donnera cette expression en fonction de
du Soleil. On donnera cette expression en fonction de 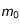 ,
, 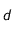 et
et  (on négligera l'effet de phase).
(on négligera l'effet de phase).
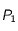 reçue et réémise par la planète est proportionnelle à
reçue et réémise par la planète est proportionnelle à 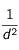 , puis que la puissance
, puis que la puissance 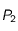 reçue au niveau de la Terre est
reçue au niveau de la Terre est 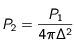
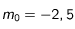 et
et 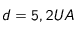 , puis à Mars pour lequel
, puis à Mars pour lequel 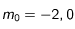 et
et 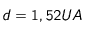 : Calculer la magnitude de ces planètes lorsqu'elles sont en
: Calculer la magnitude de ces planètes lorsqu'elles sont en 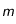 . On l'observe ensuite au travers d'un instrument dont le diamètre d'ouverture est
. On l'observe ensuite au travers d'un instrument dont le diamètre d'ouverture est 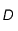 avec une pupille de sortie dont le diamètre
avec une pupille de sortie dont le diamètre 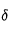 est égal à celle de l'oeil.
est égal à celle de l'oeil.
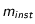 de cette étoile au travers de cet instrument.
de cette étoile au travers de cet instrument.
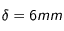
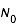 le nombre d'atomes au temps 0.
le nombre d'atomes au temps 0.
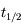 le nombre d'atomes radioactifs est-il réduit de moitié ?
le nombre d'atomes radioactifs est-il réduit de moitié ?
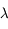 et
et 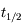 .
.
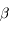 en strontium 87 avec une demi-vie de 49 milliards d'années, selon la réaction suivante :
en strontium 87 avec une demi-vie de 49 milliards d'années, selon la réaction suivante :
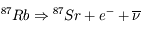
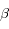 ). Le nombre de masse (87) est inchangé, le nombre de charges varie (de 37 à 38). La charge totale est conservée par l'émission d'un électron. La quatrième particule est un anti-neutrino symétrique de l'électron, dont la présence est requise par la conservation du moment cinétique.
). Le nombre de masse (87) est inchangé, le nombre de charges varie (de 37 à 38). La charge totale est conservée par l'émission d'un électron. La quatrième particule est un anti-neutrino symétrique de l'électron, dont la présence est requise par la conservation du moment cinétique.
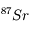 à l'instant de la mesure t en fonction des quantités de
à l'instant de la mesure t en fonction des quantités de 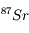 initiale et de
initiale et de 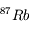 actuelle et initiale.
actuelle et initiale.
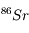 , isotope stable du strontium qui n'est pas un produit de désintégration (son abondance n'est donc pas fonction du temps). Faire apparaître ces rapports. Commentaires ?
, isotope stable du strontium qui n'est pas un produit de désintégration (son abondance n'est donc pas fonction du temps). Faire apparaître ces rapports. Commentaires ?
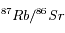
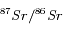
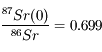
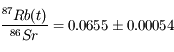
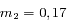
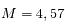
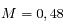
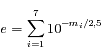 puis
puis 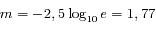
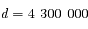 km
km
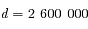 km
km
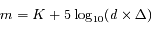 .
. 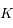 est une constante que l'on élimine par l'introduction de
est une constante que l'on élimine par l'introduction de 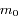 . En effet à l'
. En effet à l'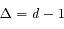 (en ua). On en déduit donc que:
(en ua). On en déduit donc que:
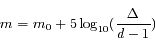
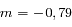
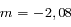
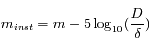
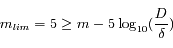
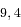 /
/ 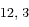 /
/ 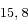 /
/ 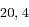
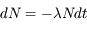
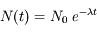
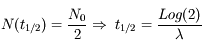
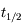 est appelé demi-vie, ou période radioactive, de l'espèce.
est appelé demi-vie, ou période radioactive, de l'espèce.
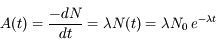
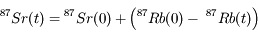
![\frac{^{87}Sr(t)}{^{86}Sr} = \frac{^{87}Sr(0)}{^{86}Sr} + \frac{^{87}Rb(t)}{^{86}Sr} + \left[ exp(\lambda t) -1 \right]](../pages_exp/equations_exp/equation77.png)
