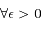 ,
, 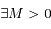 et
et 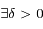 tels que
tels que 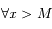 on a
on a 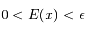 et
et 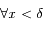 et
et 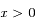 on a
on a 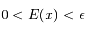 .
.
Les limites trouvées à la question précedente nous permettent de dire que 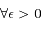 ,
, 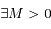 et
et 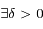 tels que
tels que 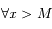 on a
on a 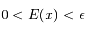 et
et 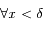 et
et 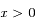 on a
on a 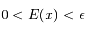 .
.
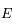 est une fonction continue sur l'intervalle
est une fonction continue sur l'intervalle ![[\delta,M]](../pages_extremas/equations_extremas/equation43.png) . Or l'image d'un segment fermé par une fonction continue est un segment fermé. Ce dernier possède donc une borne supérieure qui est atteinte par la fonction
. Or l'image d'un segment fermé par une fonction continue est un segment fermé. Ce dernier possède donc une borne supérieure qui est atteinte par la fonction 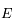 sur
sur ![[\delta,M]](../pages_extremas/equations_extremas/equation45.png) .
.
Soit 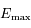 ce maximum. On peut alors choisir
ce maximum. On peut alors choisir 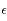 pour que
pour que 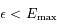 , ainsi
, ainsi 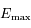 sera aussi le maximum de
sera aussi le maximum de 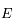 sur
sur ![]0,+\infty[](../pages_extremas/equations_extremas/equation51.png) .
.