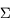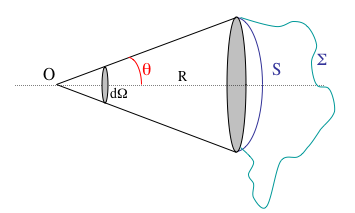
L'angle solide ne dépend que du contour sur lequel s'appuie la surface considérée, c'est-à-dire de la surface apparente. Dans la figure ci-dessous, les surfaces S et 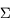\Sigma sont vues sous le même angle solide.

AS_fig1c.png
Crédit : Astrophysique sur Mesure / Erard

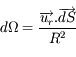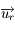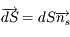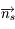Une surface élémentaire dS se confond avec la calotte sphérique correspondante. L'angle solide élémentaire est défini comme d\Omega = \frac{\overrightarrow{u_r}.\overrightarrow{dS}}{R^2} où \overrightarrow{u_r} est le vecteur unitaire sur la ligne de visée, et \overrightarrow{dS}} = dS \overrightarrow{n_s} où \overrightarrow{n_s} est le vecteur normal à la surface.

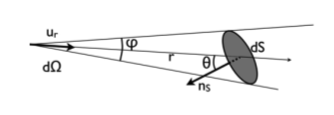
AS_fig2.png
Crédit : Astrophysique sur Mesure / Erard

Si la surface dS est inclinée d'un angle 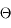\Theta sur la ligne de visée, on a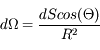 d\Omega = \frac{dS cos(\Theta)}{R^2}

On notera que cette quantité est algébrique, ce qui permet de généraliser la première remarque à toutes les surfaces s'appuyant sur le même contour : les éléments qui "dépassent" du contour sont comptés positivement puis négativement.

AS_fig1d.png
Crédit : Astrophysique sur Mesure / Erard