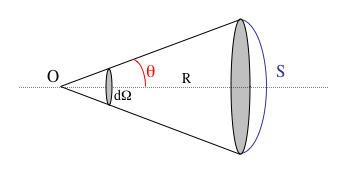
On cherche à caractériser la partie de l'espace délimitée par un cône de sommet O et de demi-ouverture 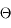 . On considère la calotte sphérique de rayon R et d'aire S(R) délimitée par ce cône. La quantité
. On considère la calotte sphérique de rayon R et d'aire S(R) délimitée par ce cône. La quantité
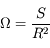
est indépendante de R. Elle mesure l'angle solide défini par le cône.
Cette quantité sans dimension est mesurée en stéradians (sr) - voir la définition des unités physiques.
 Angles solides
Angles solides
Difficulté : ☆
Temps : 30 min
Question 1)
Quel est l'angle solide sous-tendu par un demi-espace ? Par l'espace complet ?
Question 2)
Quel est l'angle solide sous-tendu par une surface quelconque, de quoi dépend-il ?
Ecrire l'application à une surface plane élémentaire dS inclinée sur la ligne de visée.
Question 3)
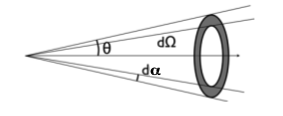
Donner l'expression différentielle de l'angle solide élémentaire en coordonnées sphériques.

Crédit :
Sharayanan/GNU Free Documentation License
Question 4)
On considère maintenant une couronne circulaire élémentaire de demi-ouverture 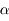 . Donner l'expression de l'angle solide en fonction de cet angle. En déduire l'angle solide sous-tendu par une calotte de demi-ouverture
. Donner l'expression de l'angle solide en fonction de cet angle. En déduire l'angle solide sous-tendu par une calotte de demi-ouverture 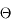 .
.
Question 5)
Que devient cette valeur si l'angle 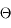 est petit ? Estimer l'angle solide sous lequel on voit le Soleil et la Lune depuis la Terre.
est petit ? Estimer l'angle solide sous lequel on voit le Soleil et la Lune depuis la Terre.
 Photométrie
Photométrie
Difficulté : ☆☆
Temps : 30 min
Question 1)
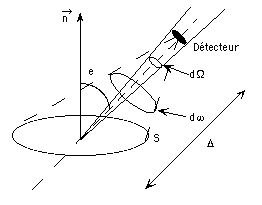
On observe une surface plane à l'aide d'une caméra, dans la configuration de la figure ci-dessous : le détecteur de la caméra a une surface 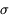 , on observe la source de surface S sous un angle e à la distance
, on observe la source de surface S sous un angle e à la distance  . Les dimensions sont telles que les angles solides considérés sont petits (
. Les dimensions sont telles que les angles solides considérés sont petits (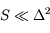 ).
).
Ecrire l'angle solide sous lequel le détecteur voit la source. Ecrire l'angle solide sous lequel la source voit la surface collectrice. Dériver une relation entre les deux angles solides.
Question 2)
On note W' la puissance lumineuse diffusée par la source par unité d'angle solide. L'éclairement (ou irradiance) est la puissance recueillie par unité de surface de détecteur en provenance de la source.
Ecrire l'éclairement E en fonction de la puissance totale reçue par le détecteur (dW). Quelle est l'unité de mesure de cette quantité dans le Système International ? De quoi dépend-elle en général ?
Question 3)
La luminance (ou intensité spécifique) d'une source est la puissance lumineuse émise ou diffusée dans un angle solide élémentaire par unité de surface apparente.
Ecrire la luminance en fonction de dW. Dans quelle unité SI se mesure cette quantité ? De quoi dépend-elle en général ?
Question 4)
Ecrire l'éclairement reçu par le détecteur en fonction de la luminance de la source et de la distance. Que signifie cette expression si la source est ponctuelle (c'est-à-dire si elle ne remplit pas le champ de l'instrument) et dans le cas contraire ?
 Intégrales angulaires
Intégrales angulaires
On trouvera ici des exercices d'intégration angulaire sur les quantités photométriques.
Auteur: Alain Vienne (et le groupe IREM de Lille1)
On se propose d'établir les conditions pour que le croissant de Lune soit vu d'un lieu de la Terre comme une gondole:
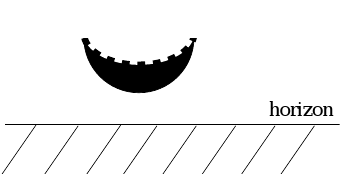
Croissant de Lune vu horizontalement (comme une "gondole").
Nous allons étudier ce problème par la trigonométrie sphérique qui permet de voir facilement les choses. La notion de sphère céleste est issue du fait que, à un lieu donné et à une date donnée, l'observateur n'a pas accès à la distance entre lui et l'objet céleste. Cet observateur peut alors considérer que tous ces objets sont à une même distance (arbitraire). Cela revient à dire que l'observateur n'appréhende que les directions issues de sa position. Or l'ensemble de ces directions s'identifie à une sphère centrée sur ce point.
Aucune formule n'est nécessaire pour résoudre l'exercice suivant. Il suffit de connaitre les bases. Soit:
- On considère une sphère de rayon 1.
- L'intersection de tout plan passant son centre avec la sphère est un grand cercle. Les grands cercles sont les géodésiques de la sphère.
- On s'oriente sur la sphère par la donnée un grand cercle orienté (ou de manière équivalente par un point appelé pôle qui est situé à 90° du grand cercle origine) et par une origine sur ce grand cercle.
Auteur: Alain Vienne
 Exercice
Exercice
Difficulté : ☆☆
Temps : 2h
Question 1)
Montrer que la condition d'horizontalité du croissant de Lune nécessite que la Lune et le Soleil aient le même azimut.
Question 2)
La condition de même azimut est donc une condition nécessaire. Réciproquement, si cette condition est réalisée, préciser les conditions sur les hauteurs du Soleil et de la Lune pour que le croissant soit vu comme une "gondole" et non à l'envers (un "D" renversé).
La hauteur est l'angle sur le vertical (cercle de même azimut). Il est compté de -90° à 90° par rapport à l'horizon.
Question 3)
Cette figure donne, pour chaque position
de la Lune sur le même vertical que le Soleil (quand la condition
est réalisée), l'aspect de celle-ci.
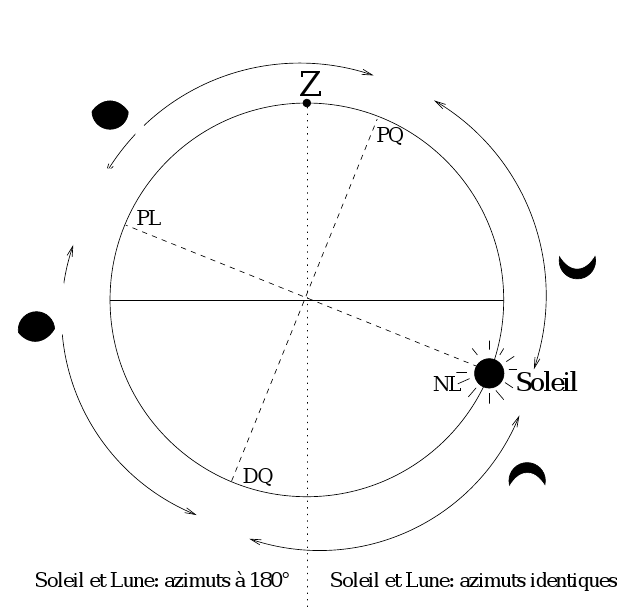
Phases de la Lune sous la condition de
même azimut. Figure dans le vertical de la Lune (et du Soleil).
La position du zénith sur le cercle est indicatif. Elle correspond
au cas de la figure donnée en solution de la question précédente. Bien-sur, si le zénith
est ailleurs sur le cercle, cela change les conditions de lever/coucher
du Soleil et de la Lune. Faites d'autres figures en changeant le zénith de place (cela déplace aussi l'horizon).
Question 4)
En supposant que la Lune est toujours sur l'écliptique, donner les seuls endroits de la Terre où il est possible de voir le croissant de Lune horizontal.
Aucun calcul n'est nécessaire pour répondre à cette question. Une discussion avec les proprietés élémentaires de la géométrie sphérique devrait suffire.
Auteur: Alain Vienne (et le groupe IREM de Lille1)
Il est peut-être plus facile de voir les 2 cas (coplanaire et non-coplanaire)
en raisonnant sur la sphère des fixes. Précédemment,
on regardait le mouvement diurne d'un point de la sphère des fixes
(le pôle 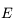 de l'écliptique) sur la sphère locale (de pôle
de l'écliptique) sur la sphère locale (de pôle 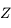 ).
Ici, nous allons faire la démarche réciproque: on regarde
le mouvement diurne de
).
Ici, nous allons faire la démarche réciproque: on regarde
le mouvement diurne de 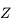 sur la sphère des fixes. On utilise la
condition suivante:
sur la sphère des fixes. On utilise la
condition suivante:
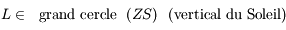
En effet, nous avons vu que c'est la condition pour voir la Lune comme
une gondole (ou tout au moins, la Lune à l'horizontal).
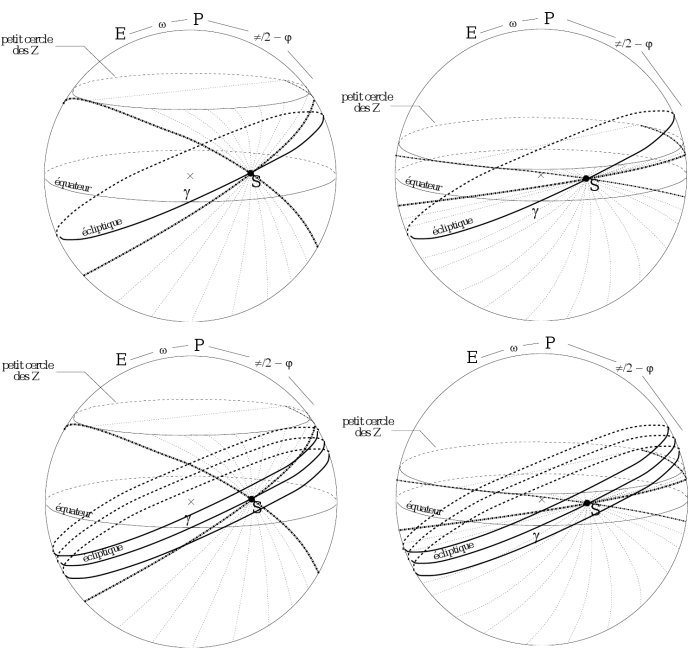
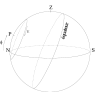
Petit cercle des zéniths sur la
sphère des fixes durant le mouvement diurne. Cas d'une zone tempérée
(à gauche) et d'une zone intertropicale (à droite). Cas de la Lune
sur l'écliptique (en haut) et cas de la Lune de part et d'autre de
l'écliptique à
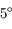
au plus (en bas).
Crédit :
Alain Vienne / IREM de Lille
Sur une sphère des fixes où on a placé l'équateur, l'écliptique et
leur pôle, et pour une latitude 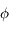 donnée, on trace le petit
cercle correspondant aux positions prises par le zénith au cours du
mouvement diurne (petit cercle des
donnée, on trace le petit
cercle correspondant aux positions prises par le zénith au cours du
mouvement diurne (petit cercle des 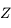 ). A chacune de
ces positions de
). A chacune de
ces positions de 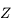 , il correspond un seul grand cercle passant
par le Soleil: c'est le vertical du Soleil. On obtient ainsi un "faisceau"
de grands cercles dont les sommets sont le Soleil et le point diamétralement
opposé. Sur la figure, pour ne
pas encombrer celle-ci, nous en avons tracé qu'une partie puisque
qu'on les a arrétés au niveau du petit cercle des
, il correspond un seul grand cercle passant
par le Soleil: c'est le vertical du Soleil. On obtient ainsi un "faisceau"
de grands cercles dont les sommets sont le Soleil et le point diamétralement
opposé. Sur la figure, pour ne
pas encombrer celle-ci, nous en avons tracé qu'une partie puisque
qu'on les a arrétés au niveau du petit cercle des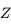 . En réalité,
ces grands cercles sont bien complets de sorte que toute la calotte
sphérique se situant au dessus du petit cercle des
. En réalité,
ces grands cercles sont bien complets de sorte que toute la calotte
sphérique se situant au dessus du petit cercle des 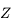 est parcouru par ces grands cercles. Ainsi
la sphère est divisée en deux parties: celle contenant chaque vertical
du Soleil et l'autre.
est parcouru par ces grands cercles. Ainsi
la sphère est divisée en deux parties: celle contenant chaque vertical
du Soleil et l'autre.
La Lune doit se trouver dans la première partie (les "faisceaux" de la figure).
La frontière entre ces deux parties correspond au vertical du Soleil
qui est tangent au petit cercle des 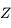 .
.
Cas de la Lune sur l'écliptique: Ce cas correspond aux 2 dessins du haut de la figure.
En dehors de la zone intertropicale (à gauche), l'écliptique coupe
les "faisceaux" qu'en ses sommets: au Soleil et au point
diamétralement opposé. Si on impose à la Lune d'être sur l'écliptique,
il n'y a qu'en ces points que la condition est réalisée (éclipses).
Par contre, dans la zone intertropicale, tout l'écliptique est contenu
dans les "faisceaux". Ainsi la condition est réalisée deux
fois par jour comme on l'a vu dans précédemment.
Cas où la Lune est de part et d'autre de l'écliptique:
L'orbite de la Lune est inclinée d'environ 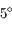 sur l'écliptique.
Son noeud qui permettrait de positionner le grand cercle correspondant
à son orbite, a un mouvement de rétrograde de
sur l'écliptique.
Son noeud qui permettrait de positionner le grand cercle correspondant
à son orbite, a un mouvement de rétrograde de 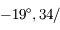 an (période:
18,6 ans). Pour ne pas rentrer dans trop de détails superflus à la
compréhension, nous allons simplement considérer que la Lune est de
part et d'autre de l'écliptique sur une bande large de
an (période:
18,6 ans). Pour ne pas rentrer dans trop de détails superflus à la
compréhension, nous allons simplement considérer que la Lune est de
part et d'autre de l'écliptique sur une bande large de 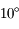 . Bien-sur,
il ne faut pas oublier que la Lune parcourt en fait un grand cercle
contenu dans cette bande: la position en longitude dans cette bande
dépend de la date dans la lunaison et la position "verticale"
dans cette bande dépend de la position du noeud de l'orbite lunaire.
. Bien-sur,
il ne faut pas oublier que la Lune parcourt en fait un grand cercle
contenu dans cette bande: la position en longitude dans cette bande
dépend de la date dans la lunaison et la position "verticale"
dans cette bande dépend de la position du noeud de l'orbite lunaire.
On remarque ainsi qu'au voisinage de la pleine Lune ou au voisinage
de la nouvelle Lune, la condition de "Lune horizontale"
est possible partout sur la Terre.
Mais on se rend bien compte que, loin des tropiques, la zone est étroite. Elle s'agrandit
au fur et à mesure que le lieu considéré s'approche du tropique.
Dans le cas d'un lieu dans la zone intertropicale, la possibilité
d'une telle condition est grande. La probabilité de réalisation l'est
donc aussi. Cependant cette probabilité n'est pas 1, car on voit
apparaitre une petite zone de la bande lunaire qui croise la partie
où il n'y a pas de vertical du Soleil (en dehors des "faisceaux").
Cette zone est petite et proche du Soleil. Ainsi même dans la zone
intertropicale, il peut y avoir des jours où la Lune n'est pas vue
à l'horizontal. Cela se produit pour des positions particulières de
l'orbite lunaire et pour des dates proches de la pleine Lune ou de
la nouvelle Lune.
-
Question 1
Solution :
Il ressort de la définition de la page précédente que 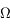 est aussi égal à l'aire de la calotte découpée par le cône sur la sphère de centre O et de rayon unité.
est aussi égal à l'aire de la calotte découpée par le cône sur la sphère de centre O et de rayon unité.
On en déduit immédiatement qu'un demi-espace sous-tend un angle solide de 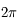 sr, et que l'espace complet sous-tend un angle solide de
sr, et que l'espace complet sous-tend un angle solide de 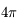 sr.
sr.
-
Question 2
Solution :
L'angle solide ne dépend que du contour sur lequel s'appuie la surface considérée, c'est-à-dire de la surface apparente. Dans la figure ci-dessous, les surfaces S et 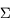 sont vues sous le même angle solide.
sont vues sous le même angle solide.
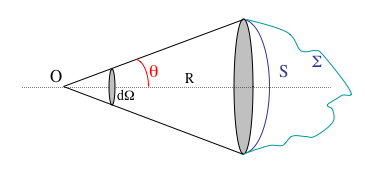
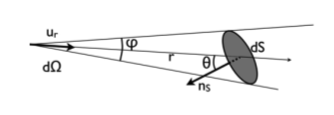
Une surface élémentaire dS se confond avec la calotte sphérique correspondante.
L'angle solide élémentaire est défini comme 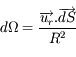 où
où 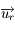 est le vecteur unitaire sur la ligne de visée, et
est le vecteur unitaire sur la ligne de visée, et 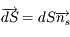 où
où 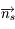 est le vecteur normal à la surface.
est le vecteur normal à la surface.
Si la surface dS est inclinée d'un angle 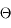 sur la ligne de visée, on a
sur la ligne de visée, on a 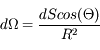
On notera que cette quantité est algébrique, ce qui permet de généraliser la première remarque à toutes les surfaces s'appuyant sur le même contour : les éléments qui "dépassent" du contour sont comptés positivement puis négativement.
-
Question 3
Solution :
A partir de l'expression de l'élément de surface, on trouve immédiatement :
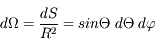
-
Question 4
Solution :
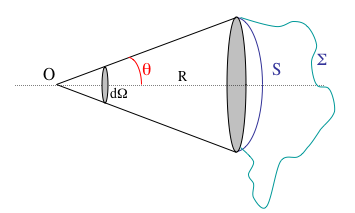
Puisqu'il y a symétrie de révolution, on intègre l'expression précédente le long de la couronne :
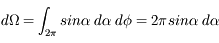
En intégrant ensuite l'angle 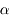 entre 0 et
entre 0 et 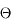 , on trouve l'angle solide défini par une calotte de demi-ouverture
, on trouve l'angle solide défini par une calotte de demi-ouverture 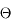 :
:
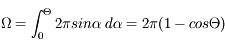
-
Question 5
Solution :
Pour les petites ouvertures, on a 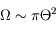 (où
(où 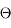 est donné en radians). Pour les très petits angles, on donne couramment les valeurs en
est donné en radians). Pour les très petits angles, on donne couramment les valeurs en 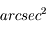 (secondes d'arc carrées) ou en
(secondes d'arc carrées) ou en 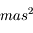 (milliarcsecondes carrées).
(milliarcsecondes carrées).
La taille apparente du Soleil et de la Lune vus depuis la Terre est d'environ 30' = 0,5°. L'angle solide correspondant est 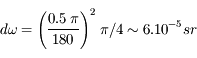
-
Question 1
Solution :
Par la figure, on se rend compte que pour voir le croissant de Lune horizontal il est nécessaire et suffisant que le Soleil éclaire la Lune par au-dessous c'est à dire qu'ils aient le même azimut.
-
Question 2
Solution :
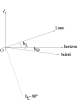
Tout d'abord, il est préférable que le Soleil soit couché et donc
sa hauteur doit être négative. La Lune, quant à elle, doit être levée:
sa hauteur est donc positive.
Soit 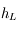 la hauteur de la Lune et
la hauteur de la Lune et 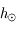 la hauteur du Soleil.
la hauteur du Soleil.
Si 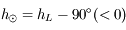 l'observateur voit exactement une demi-lune.
l'observateur voit exactement une demi-lune.
Ainsi pour avoir l'aspect indiqué sur la figure (un croissant comme
une gondole), il est nécessaire d'avoir 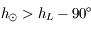 .
.
-
Question 3
-
Question 4
Aide :
Aucun calcul n'est nécessaire pour répondre à cette question. Une discussion avec les proprietés élémentaires de la géométrie sphérique devrait suffire.
Aide :
On sait qu'il n'y a qu'un seul grand cercle passant par deux points
de la sphère céleste. Or, la Lune et le Soleil sont sur un même grand
cercle (écliptique), et puisque 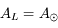 , les grands cercles
, les grands cercles
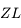 et
et 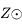 sont les mêmes. Ainsi le zénith
sont les mêmes. Ainsi le zénith 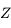 est sur l'écliptique.
est sur l'écliptique.
Aide :
"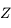 est sur l'écliptique"
est sur l'écliptique" 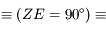 "
"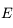 est sur l'horizon".
est sur l'horizon".
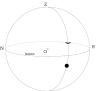
où 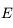 est le pôle de l'écliptique.
est le pôle de l'écliptique. 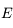 est un point de la sphère
des fixes (c'est à dire, lié aus étoiles). A ce titre, et comme toutes les étoiles, il est affecté
par le mouvement diurne.
est un point de la sphère
des fixes (c'est à dire, lié aus étoiles). A ce titre, et comme toutes les étoiles, il est affecté
par le mouvement diurne. 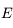 tourne autour du pôle céleste nord
tourne autour du pôle céleste nord 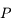 (fixe) à une même distance angulaire
(fixe) à une même distance angulaire 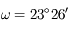 (obliquité) .
(obliquité) .
Solution :
La hauteur du pôle sur l'horizon correspond à la latitude du lieu (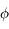 ).
).
On voit alors que pour une latitude comme celle de Lille (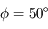 ),
cela est impossible. Ce n'est possible que si
),
cela est impossible. Ce n'est possible que si 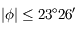 c'est à dire, entre les tropiques. En ces lieux, la condition est
réalisée 2 fois par jour.
c'est à dire, entre les tropiques. En ces lieux, la condition est
réalisée 2 fois par jour.
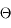 . On considère la calotte sphérique de rayon R et d'aire S(R) délimitée par ce cône. La quantité
. On considère la calotte sphérique de rayon R et d'aire S(R) délimitée par ce cône. La quantité
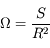

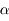 . Donner l'expression de l'angle solide en fonction de cet angle. En déduire l'angle solide sous-tendu par une calotte de demi-ouverture
. Donner l'expression de l'angle solide en fonction de cet angle. En déduire l'angle solide sous-tendu par une calotte de demi-ouverture 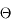 .
.
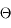 est petit ? Estimer l'angle solide sous lequel on voit le Soleil et la Lune depuis la Terre.
est petit ? Estimer l'angle solide sous lequel on voit le Soleil et la Lune depuis la Terre.
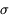 , on observe la source de surface S sous un angle e à la distance
, on observe la source de surface S sous un angle e à la distance  . Les dimensions sont telles que les angles solides considérés sont petits (
. Les dimensions sont telles que les angles solides considérés sont petits (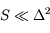 ).
).


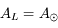 , les grands cercles
, les grands cercles
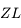 et
et 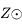 sont les mêmes. Ainsi le zénith
sont les mêmes. Ainsi le zénith 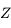 est sur l'écliptique.
est sur l'écliptique.
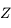 est sur l'écliptique"
est sur l'écliptique" 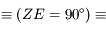 "
"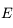 est sur l'horizon".
est sur l'horizon".
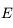 est le pôle de l'
est le pôle de l'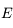 est un point de la sphère
des fixes (c'est à dire, lié aus étoiles). A ce titre, et comme toutes les étoiles, il est affecté
par le mouvement diurne.
est un point de la sphère
des fixes (c'est à dire, lié aus étoiles). A ce titre, et comme toutes les étoiles, il est affecté
par le mouvement diurne. 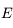 tourne autour du pôle céleste nord
tourne autour du pôle céleste nord 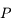 (fixe) à une même distance angulaire
(fixe) à une même distance angulaire 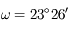 (obliquité) .
(obliquité) .
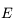 de l'écliptique) sur la sphère locale (de pôle
de l'écliptique) sur la sphère locale (de pôle 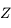 ).
Ici, nous allons faire la démarche réciproque: on regarde
le mouvement diurne de
).
Ici, nous allons faire la démarche réciproque: on regarde
le mouvement diurne de 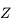 sur la sphère des fixes. On utilise la
condition suivante:
sur la sphère des fixes. On utilise la
condition suivante:
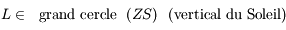

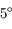 au plus (en bas).
au plus (en bas).
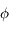 donnée, on trace le petit
cercle correspondant aux positions prises par le zénith au cours du
mouvement diurne (petit cercle des
donnée, on trace le petit
cercle correspondant aux positions prises par le zénith au cours du
mouvement diurne (petit cercle des 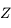 ). A chacune de
ces positions de
). A chacune de
ces positions de 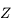 , il correspond un seul grand cercle passant
par le Soleil: c'est le vertical du Soleil. On obtient ainsi un "faisceau"
de grands cercles dont les sommets sont le Soleil et le point diamétralement
opposé. Sur la figure, pour ne
pas encombrer celle-ci, nous en avons tracé qu'une partie puisque
qu'on les a arrétés au niveau du petit cercle des
, il correspond un seul grand cercle passant
par le Soleil: c'est le vertical du Soleil. On obtient ainsi un "faisceau"
de grands cercles dont les sommets sont le Soleil et le point diamétralement
opposé. Sur la figure, pour ne
pas encombrer celle-ci, nous en avons tracé qu'une partie puisque
qu'on les a arrétés au niveau du petit cercle des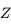 . En réalité,
ces grands cercles sont bien complets de sorte que toute la calotte
sphérique se situant au dessus du petit cercle des
. En réalité,
ces grands cercles sont bien complets de sorte que toute la calotte
sphérique se situant au dessus du petit cercle des 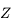 est parcouru par ces grands cercles. Ainsi
la sphère est divisée en deux parties: celle contenant chaque vertical
du Soleil et l'autre.
est parcouru par ces grands cercles. Ainsi
la sphère est divisée en deux parties: celle contenant chaque vertical
du Soleil et l'autre.
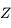 .
.
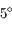 sur l'écliptique.
Son noeud qui permettrait de positionner le grand cercle correspondant
à son orbite, a un mouvement de rétrograde de
sur l'écliptique.
Son noeud qui permettrait de positionner le grand cercle correspondant
à son orbite, a un mouvement de rétrograde de 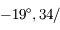 an (période:
18,6 ans). Pour ne pas rentrer dans trop de détails superflus à la
compréhension, nous allons simplement considérer que la Lune est de
part et d'autre de l'écliptique sur une bande large de
an (période:
18,6 ans). Pour ne pas rentrer dans trop de détails superflus à la
compréhension, nous allons simplement considérer que la Lune est de
part et d'autre de l'écliptique sur une bande large de 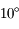 . Bien-sur,
il ne faut pas oublier que la Lune parcourt en fait un grand cercle
contenu dans cette bande: la position en longitude dans cette bande
dépend de la date dans la lunaison et la position "verticale"
dans cette bande dépend de la position du noeud de l'orbite lunaire.
. Bien-sur,
il ne faut pas oublier que la Lune parcourt en fait un grand cercle
contenu dans cette bande: la position en longitude dans cette bande
dépend de la date dans la lunaison et la position "verticale"
dans cette bande dépend de la position du noeud de l'orbite lunaire.
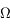 est aussi égal à l'aire de la calotte découpée par le cône sur la sphère de centre O et de rayon unité.
est aussi égal à l'aire de la calotte découpée par le cône sur la sphère de centre O et de rayon unité.
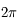 sr, et que l'espace complet sous-tend un angle solide de
sr, et que l'espace complet sous-tend un angle solide de 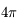 sr.
sr.
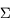 sont vues sous le même angle solide.
sont vues sous le même angle solide.
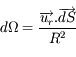 où
où 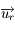 est le vecteur unitaire sur la ligne de visée, et
est le vecteur unitaire sur la ligne de visée, et 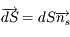 où
où 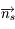 est le vecteur normal à la surface.
est le vecteur normal à la surface.
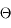 sur la ligne de visée, on a
sur la ligne de visée, on a 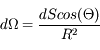
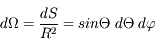
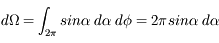
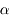 entre 0 et
entre 0 et 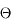 , on trouve l'angle solide défini par une calotte de demi-ouverture
, on trouve l'angle solide défini par une calotte de demi-ouverture 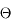 :
:
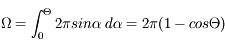
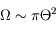 (où
(où 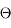 est donné en radians). Pour les très petits angles, on donne couramment les valeurs en
est donné en radians). Pour les très petits angles, on donne couramment les valeurs en 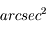 (secondes d'arc carrées) ou en
(secondes d'arc carrées) ou en 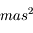 (milliarcsecondes carrées).
(milliarcsecondes carrées).
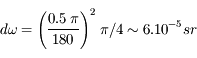
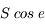 .
.
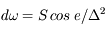
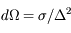
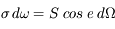
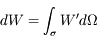
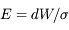
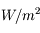 . Elle suppose une géométrie d'observation donnée (angle d'incidence sur le détecteur et distance à la source).
. Elle suppose une géométrie d'observation donnée (angle d'incidence sur le détecteur et distance à la source).
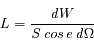
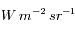 . Il s’agit d'une caractéristique intrinsèque à la source lumineuse, qui dépend a priori de la direction d'observation e.
. Il s’agit d'une caractéristique intrinsèque à la source lumineuse, qui dépend a priori de la direction d'observation e.
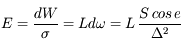
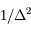 . C'est le cas des objets lointains non résolus, par exemple les étoiles observées au télescope.
. C'est le cas des objets lointains non résolus, par exemple les étoiles observées au télescope.
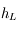 la hauteur de la Lune et
la hauteur de la Lune et 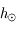 la hauteur du Soleil.
la hauteur du Soleil.
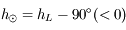 l'observateur voit exactement une demi-lune.
l'observateur voit exactement une demi-lune.
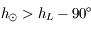 .
.
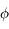 ).
).
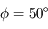 ),
cela est impossible. Ce n'est possible que si
),
cela est impossible. Ce n'est possible que si 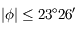 c'est à dire, entre les tropiques. En ces lieux, la condition est
réalisée 2 fois par jour.
c'est à dire, entre les tropiques. En ces lieux, la condition est
réalisée 2 fois par jour.