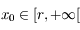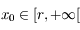Soit x_0\in[r,+\infty[, on a:

g(x)=f(x)-[f(x_0)+f'(x_0)(x-x_0)].

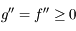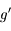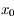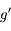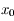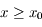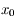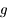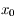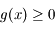On remarque facilement que g(x_0)=0, g'(x_0)=0 et g''=f''\ge0. Ainsi g' est une fonction croissante au voisinage de x_0, donc g' est négative pour x\gex_0 et positive pour x\ge x_0. Donc x_0 correspond à un minimum pour g. Ainsi au voisinage de x_0 on a g(x)\ge 0 ce qui montre que la courbe représentative de 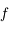f est effectivement au-dessus de sa tangente.