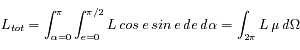
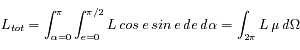
Chaque élément de surface rayonne en L cos e. En intégrant dans toutes les directions on trouve : L_{tot} = \int_{\alpha=0}^{\pi} \int_{e=0}^{\pi/2} L\,cos\,e\,sin\,e\,de\,d\alpha = \int_{2\pi} L\,\mu\,d\Omega

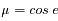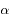où \mu = cos \, e, et \alpha est l'azimuth. L'intégrale porte sur le demi-espace libre (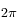2 \pi sr).

On a de façon évidente 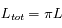L_{tot} = \pi L puisque la luminance L est isotrope par hypothèse.

On remarque que la quantité L est intensive (non sommable). La quantité 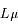L \mu est la puissance diffusée par unité de surface, qui est sommable.