Les surfaces planétaires réfléchissent la lumière solaire d'une façon qui dépend de leurs propriétés et de leur composition. Si les caractéristiques spectrales reflètent la composition (minéralogique) d'une surface, la distribution angulaire du rayonnement diffusé dépend surtout de ses propriétés physiques : taille de particules, porosité, rugosité à diverses échelles...
Divers modèles photométriques rendent compte de ces comportements, en décrivant la dépendance angulaire de la luminance. La luminance est la puissance émise ou diffusée dans un angle solide élémentaire par unité de surface. Il s’agit d’une caractéristique intrinsèque à la source lumineuse :
Figure 1
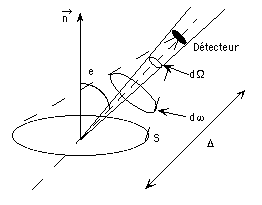
Géométrie d'observation d'une surface
Dans la configuration générale décrite Figure 1, la luminance est définie de la façon suivante :
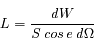
où dW est la puissance recueillie par le détecteur, e est l'angle sous lequel on voit la source, 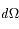 l'angle solide sous lequel la source voit le détecteur, et S la surface de la source. Dans le Système International, la luminance se mesure en
l'angle solide sous lequel la source voit le détecteur, et S la surface de la source. Dans le Système International, la luminance se mesure en 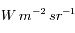 , ou dans un intervalle de longueur d'onde élémentaire en
, ou dans un intervalle de longueur d'onde élémentaire en 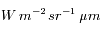 .
.
Le modèle photométrique le plus commun est le modèle lambertien, que suit notamment le corps noir : la luminance est simplement isotrope (ne dépend pas de la direction e).
 Soleil
Soleil
Difficulté : ☆☆
Temps : 45 min
Question 1)
On assimile le Soleil à un corps noir. Quelle est la puissance rayonnée par un élément de surface dans une direction donnée ?
En première approximation, le Soleil rayonne comme un corps noir à la température de la photosphère (5780 K en moyenne).
Question 2)
Calculer la luminance intégrale (intégrée spectralement), toujours dans une direction donnée. Application numérique.
Question 3)
Calculer la luminosité totale d'un élément de surface (rayonnée dans toutes les directions). Commenter.
Question 4)
Calculer la puissance totale émise par le Soleil. Application numérique (on donne pour le rayon du Soleil 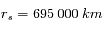 ).
).
 Surface lunaire
Surface lunaire
Difficulté : ☆☆
Temps : 20 min
Le cas des surfaces planétaires est différent, leur capacité à réfléchir le rayonnement solaire dépendant de leur état physique : rugosité, taille des particules en surface... En outre la position du Soleil intervient également puisqu'on observe maintenant en réflexion (voir Figure 2). Le modèle lambertien est encore adapté aux surfaces très claires, mais ne décrit pas correctement les propriétés de la Lune ou des astéroïdes qui sont relativement sombres. On utilise souvent le modèle de Lommel-Seeliger, qui donne la luminance comme :
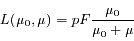
où p est l'albedo de la surface (coefficient de réflexion sous incidence et émergence nulles), F est le flux solaire à la distance de la planète, 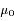 et
et 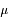 sont les cosinus des angles d'incidence et d'émergence.
sont les cosinus des angles d'incidence et d'émergence.
Figure 2
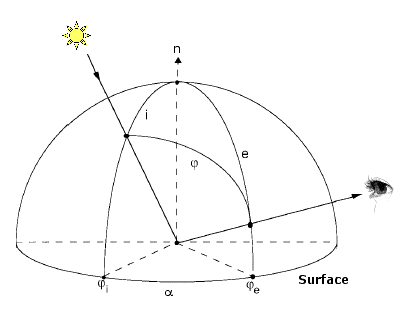
Géométrie d'observation d'une surface planétaire
Question 1)
On utilise la réflectance hémisphérique pour étudier les propriétés thermiques des surfaces. Celle-ci est définie comme :
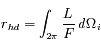
où 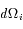 est l'angle solide élémentaire dans la direction d'incidence.
est l'angle solide élémentaire dans la direction d'incidence.
Calculer cette quantité en fonction des variables 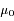 et
et 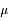 .
.
Auteur : Marc Fouchard.
Le but de cet exercice est de montrer qu'un volume soumis à un flux, c'est-à-dire qu'en chaque point de l'espace on peut associer un vecteur vitesse donné par une équation différentielle d'ordre 1, hamiltonien reste constant.
La figure suivante illustre cette propriété dans le cas du problème de 2 corps plan. Comme on est à deux dimensions un volume correspond à une surface. Le disque est soumis à une force gravitationelle due à un corps massif se trouvant à l'origine. La surface verte est constante au cours du temps, même si la forme est fortement modifiée.
théorème de Liouville
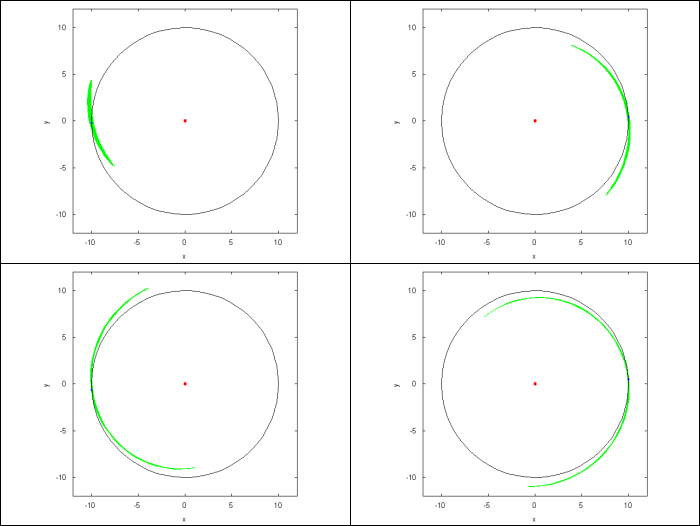
Un flux hamiltonien vérifie les équations d'hamilton. C'est-à-dire que le point de coordonnées 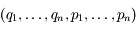 vérifie les équations différentielles suivantes :
vérifie les équations différentielles suivantes :
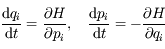 , avec
, avec 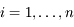 .
.
où 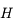 est le hamiltonien du système, indépendant du temps.
est le hamiltonien du système, indépendant du temps.
Auteur: Marc Fouchard
 théorème de Liouville
théorème de Liouville
Difficulté : ☆☆☆
Temps : 1h
Question 2)
Montrer que 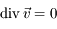 et donc que
et donc que 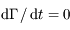 .
.
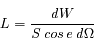
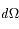 l'angle solide sous lequel la source voit le détecteur, et S la surface de la source. Dans le Système International, la luminance se mesure en
l'angle solide sous lequel la source voit le détecteur, et S la surface de la source. Dans le Système International, la luminance se mesure en 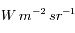 , ou dans un intervalle de longueur d'onde élémentaire en
, ou dans un intervalle de longueur d'onde élémentaire en 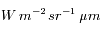 .
.

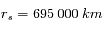 ).
).
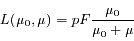
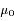 et
et 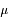 sont les cosinus des angles d'incidence et d'émergence.
sont les cosinus des angles d'incidence et d'émergence.

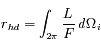
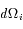 est l'angle solide élémentaire dans la direction d'incidence.
est l'angle solide élémentaire dans la direction d'incidence.
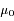 et
et 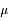 .
.

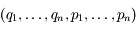 vérifie les équations différentielles suivantes :
vérifie les équations différentielles suivantes :
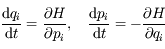 , avec
, avec 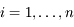 .
.
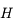 est le hamiltonien du système, indépendant du temps.
est le hamiltonien du système, indépendant du temps.
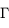 un volume de surface
un volume de surface 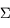 . La variation du volume au cours du temps s'écrit:
. La variation du volume au cours du temps s'écrit:
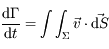 ,
,
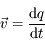 est le vecteur vitesse et
est le vecteur vitesse et 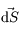 est un vecteur normal à la surface
est un vecteur normal à la surface 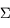 et de norme égale à une élément de surface.
et de norme égale à une élément de surface.
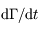 en vonction de la divergence de la vitesse
en vonction de la divergence de la vitesse 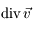 .
.
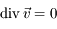 et donc que
et donc que 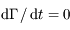 .
.
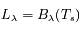
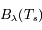 est la fonction de Plank pour la température de la photosphère. Il s'agit de la luminosité d'un élément de surface dans un intervalle de longueur d'onde et dans une direction donnée.
est la fonction de Plank pour la température de la photosphère. Il s'agit de la luminosité d'un élément de surface dans un intervalle de longueur d'onde et dans une direction donnée.
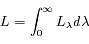
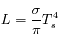 =
= 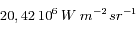
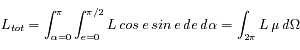
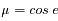 , et
, et 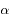 est l'azimuth. L'intégrale porte sur le demi-espace libre (
est l'azimuth. L'intégrale porte sur le demi-espace libre (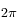 sr).
sr).
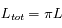 puisque la luminance L est isotrope par hypothèse.
puisque la luminance L est isotrope par hypothèse.
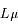 est la puissance diffusée par unité de surface, qui est sommable.
est la puissance diffusée par unité de surface, qui est sommable.
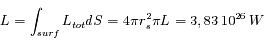
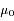 , le résultat est donc une fonction de
, le résultat est donc une fonction de 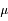 seul:
seul:
![r_{hd}(\mu) = 2p \left[ 1 - \mu Log \frac{\mu +1}{\mu} \right]](../pages_int-mult/equations_int-mult/equation27.png)
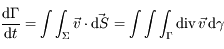 .
.
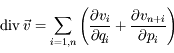 .
.
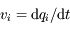 et
et 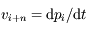 , donc en tenant compte des propriétés du flux hamiltonien données dans l'introduction on a:
, donc en tenant compte des propriétés du flux hamiltonien données dans l'introduction on a:
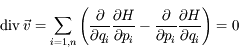 .
.