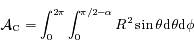 ,
où
,
où 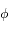 est l'angle
est l'angle 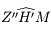 et
et 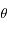 l'angle
l'angle 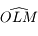 avec
avec 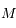 un point de la calotte,
un point de la calotte, 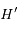 son projeté orthogonal sur la droite
son projeté orthogonal sur la droite 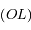 et
et 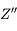 le point de la droite
le point de la droite 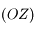 dont la projection orthogonale sur
dont la projection orthogonale sur 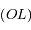 est
est 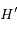 .
.
On doit calculer l'intégrale:
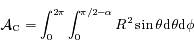 ,
où
,
où 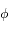 est l'angle
est l'angle 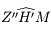 et
et 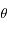 l'angle
l'angle 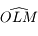 avec
avec 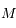 un point de la calotte,
un point de la calotte, 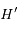 son projeté orthogonal sur la droite
son projeté orthogonal sur la droite 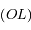 et
et 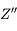 le point de la droite
le point de la droite 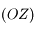 dont la projection orthogonale sur
dont la projection orthogonale sur 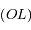 est
est 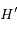 .
.
On trouve:
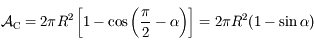 .
C'est-à-dire:
.
C'est-à-dire:
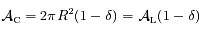 .
.