Auteur : Jérôme Thiébaut
En coordonnées cartésiennes, un élément de longueur 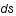 se calcule selon le théorème de Pythagore:
se calcule selon le théorème de Pythagore:
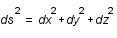 .
.
Ceci donne en coordonnées sphériques:
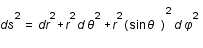 .
.
On voit que l'expression de 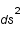 dépend de la métrique utilisée, c'est à dire de la manière de décrire l'espace.
En cosmologie, dans le cadre de la relativité générale, on calcule de même les éléments de longueur en fonction de la métrique de l'espace temps soit:
dépend de la métrique utilisée, c'est à dire de la manière de décrire l'espace.
En cosmologie, dans le cadre de la relativité générale, on calcule de même les éléments de longueur en fonction de la métrique de l'espace temps soit:
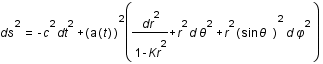 ,
,
ou 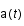 est le facteur d'échelle qui décrit l'expansion de l'univers,
est le facteur d'échelle qui décrit l'expansion de l'univers, 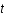 le temps,
le temps, 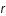 ,
, 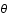 et
et 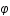 les coordonnées comobiles (c'est à dire fixes par rapport à l'expansion de l'univers) ,
les coordonnées comobiles (c'est à dire fixes par rapport à l'expansion de l'univers) , 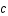 la vitesse de la lumière et
la vitesse de la lumière et 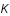 la courbure de l'univers.
la courbure de l'univers.
Pour un photon, la trajectoire est telle que 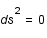 .
.
On se propose dans cet exercice d'étudier la trajectoire d'un photon radial afin de relier le redshift (ou décallage spectral), 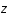 , au facteur d'échelle,
, au facteur d'échelle, 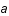 .
.
Auteur: Jérôme Thiébaut
 Redshift
Redshift
Difficulté : ☆☆
Temps : 20mn
On considère un photon radial émis à une distance 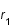 au temps
au temps 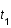 par une galaxie lointaine. Ce photon nous est reçu au temps
par une galaxie lointaine. Ce photon nous est reçu au temps 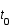 en
en 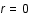 .
.
Sa trajectoire est décrite par la métrique: 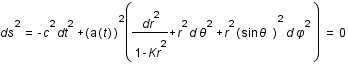 .
.
Question 1)
Simplifier la métrique compte tenu de la nature du photon et exprimer l'égalité sous forme intégrale.
Le photon étant radial, 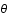 et
et 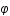 sont donc constants au cours de la trajectoire et peuvent être choisis comme nuls.
sont donc constants au cours de la trajectoire et peuvent être choisis comme nuls.
Question 2)
Un deuxième photon est émis à 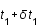 et est reçu en
et est reçu en 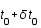 . Quelle est la nouvelle égalité sous forme intégrale ?
. Quelle est la nouvelle égalité sous forme intégrale ?
Question 3)
Sachant que 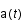 est considéré comme constant pendant un temps
est considéré comme constant pendant un temps 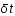 faible et que la distance comobile (
faible et que la distance comobile (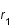 ) est constante par définition, montrer que
) est constante par définition, montrer que 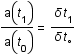 .
.
Décomposer l'intégrale par la relation de Chasles.
Auteur: Marc Fouchard
 Calotte sphérique
Calotte sphérique
Difficulté : ☆
Temps : 30 mn
Question 1)
Faire la figure qui correspond à l'énoncé.
Auteur : Alain Vienne
Le potentiel gravitaionnel de la Terre est souvent modélisé par:
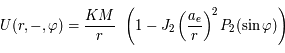
avec 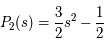
C'est le potentiel évalué en un point 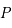 de coordonnées sphériques
de coordonnées sphériques 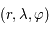 (dont le plan horizontal est la plan de l'équateur).
(dont le plan horizontal est la plan de l'équateur).
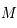 est la masse totale de la Terre et
est la masse totale de la Terre et 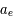 son rayon équatorial (
son rayon équatorial (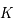 la constante de gravitation universelle).
la constante de gravitation universelle). 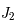 est un coefficient qui caractérise l'aplatissement de la Terre suivant l'axe des pôles. Sa valeur (sans unité) est de
est un coefficient qui caractérise l'aplatissement de la Terre suivant l'axe des pôles. Sa valeur (sans unité) est de 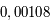 .
.
Dans l'exercice qui suit, nous allons évaluer le potentiel d'un anneau massif et homogène. Nous verrons que l'expression obtenue aura exactement la même forme que celle ci-dessus.
Un exemple d'application concerne la prise en compte de la gravitation des anneaux de Saturne: il suffit de réévaluer le cooefficient d'aplatissement 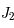 de Saturne.
de Saturne.
Voici un autre exercice sur le potentiel gravitationnel terrestre.
Auteur: Alain Vienne
 Potentiel gravitationnel de la Terre
Potentiel gravitationnel de la Terre
Difficulté : ☆
Temps : 1h
Question 2)
Calculer 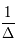 en se limitant aux termes de degré 2 au plus en
en se limitant aux termes de degré 2 au plus en 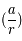 .
.
Question 4)
En comparant cette expression avec celle utilisant le coefficient 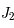 , donner le rayon de l'anneau correspondant au potentiel terrestre. On donne
, donner le rayon de l'anneau correspondant au potentiel terrestre. On donne 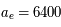 km.
km.
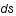 se calcule selon le théorème de Pythagore:
se calcule selon le théorème de Pythagore:
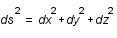 .
.
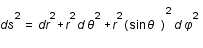 .
.
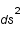 dépend de la métrique utilisée, c'est à dire de la manière de décrire l'espace.
En cosmologie, dans le cadre de la relativité générale, on calcule de même les éléments de longueur en fonction de la métrique de l'espace temps soit:
dépend de la métrique utilisée, c'est à dire de la manière de décrire l'espace.
En cosmologie, dans le cadre de la relativité générale, on calcule de même les éléments de longueur en fonction de la métrique de l'espace temps soit:
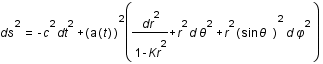 ,
,
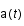 est le facteur d'échelle qui décrit l'expansion de l'univers,
est le facteur d'échelle qui décrit l'expansion de l'univers, 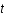 le temps,
le temps, 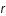 ,
, 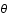 et
et 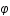 les coordonnées comobiles (c'est à dire fixes par rapport à l'expansion de l'univers) ,
les coordonnées comobiles (c'est à dire fixes par rapport à l'expansion de l'univers) , 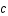 la vitesse de la lumière et
la vitesse de la lumière et 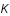 la courbure de l'univers.
la courbure de l'univers.
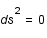 .
.
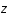 , au facteur d'échelle,
, au facteur d'échelle, 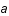 .
.
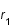 au temps
au temps 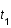 par une galaxie lointaine. Ce photon nous est reçu au temps
par une galaxie lointaine. Ce photon nous est reçu au temps 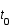 en
en 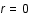 .
.
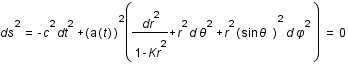 .
.
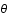 et
et 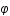 sont donc constants au cours de la trajectoire et peuvent être choisis comme nuls.
sont donc constants au cours de la trajectoire et peuvent être choisis comme nuls.
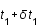 et est reçu en
et est reçu en 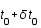 . Quelle est la nouvelle égalité sous forme intégrale ?
. Quelle est la nouvelle égalité sous forme intégrale ?
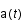 est considéré comme constant pendant un temps
est considéré comme constant pendant un temps 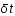 faible et que la distance comobile (
faible et que la distance comobile (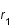 ) est constante par définition, montrer que
) est constante par définition, montrer que 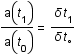 .
.
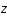 est défini comme suit:
est défini comme suit:
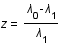 , où
, où 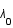 est la longueur d'onde du photon reçu et
est la longueur d'onde du photon reçu et 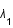 celle du photon émis.
celle du photon émis.
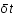 correspond une longueur d'onde
correspond une longueur d'onde 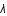 , et que par convention,
, et que par convention, 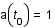 , relier la quantité
, relier la quantité 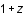 au facteur d'échelle.
au facteur d'échelle.
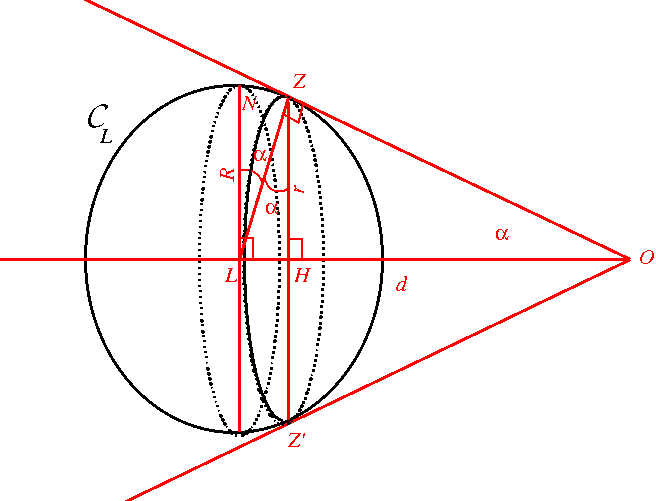
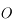 l'observateur,
l'observateur, 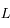 le centre de la Lune et
le centre de la Lune et 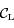 l'intersection de la sphère correspondant à la Lune avec un plan contenant la droite
l'intersection de la sphère correspondant à la Lune avec un plan contenant la droite 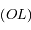 . Ainsi
. Ainsi 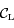 est un cercle de centre
est un cercle de centre 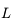 et de rayon
et de rayon 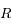 , où
, où 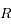 est le rayon de la Lune. On note
est le rayon de la Lune. On note 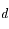 la distance
la distance 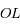 . Les tangentes à
. Les tangentes à 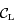 passant par
passant par 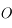 coupent
coupent 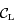 en
en 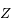 et
et 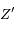 . Soit
. Soit 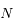 le point de
le point de 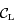 tel que
tel que 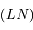 est perpendiculaire à
est perpendiculaire à 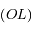 avec
avec 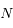 du même coté que
du même coté que 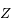 de la droite
de la droite 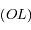 . On note
. On note 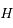 le projeté orthogonal de
le projeté orthogonal de 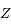 sur
sur 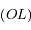 ,
, 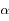 l'angle
l'angle 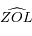 et
et 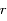 la distance
la distance 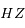 .
.
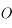 correspond donc à la partie de la surface de la Lune tournée vers
correspond donc à la partie de la surface de la Lune tournée vers 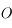 et de frontière le cercle de centre
et de frontière le cercle de centre 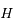 et de rayon
et de rayon 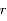 .
.
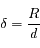 , calculer
, calculer 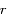 en fonction de
en fonction de 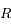 et
et 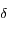 .
.
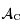 de la calotte visible depuis
de la calotte visible depuis 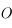 en fonction de la surface d'un hémisphère de la Lune
en fonction de la surface d'un hémisphère de la Lune 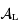 et de
et de 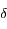 .
.
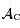 de la Terre visible par l'astronaute s'écrit sous la forme de la surface d'un cercle dont on déterminera le rayon en fonction du rayon de la Terre
de la Terre visible par l'astronaute s'écrit sous la forme de la surface d'un cercle dont on déterminera le rayon en fonction du rayon de la Terre 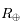 et de l'altitude
et de l'altitude 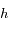 de l'astronaute. On supposera donc que
de l'astronaute. On supposera donc que 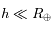 .
.
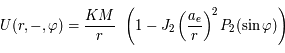
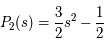
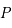 de coordonnées sphériques
de coordonnées sphériques 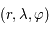 (dont le plan horizontal est la plan de l'équateur).
(dont le plan horizontal est la plan de l'équateur).
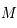 est la masse totale de la Terre et
est la masse totale de la Terre et 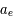 son rayon équatorial (
son rayon équatorial (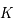 la constante de gravitation universelle).
la constante de gravitation universelle). 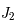 est un coefficient qui caractérise l'aplatissement de la Terre suivant l'axe des pôles. Sa valeur (sans unité) est de
est un coefficient qui caractérise l'aplatissement de la Terre suivant l'axe des pôles. Sa valeur (sans unité) est de 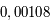 .
.
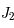 de Saturne.
de Saturne.
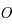 et de rayon
et de rayon 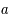 . On repère un point
. On repère un point 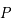 de coordonnées sphériques
de coordonnées sphériques 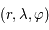 (dont le plan horizontal est le plan de l'anneau).
(dont le plan horizontal est le plan de l'anneau).
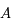 un point de l'anneau. Il fait un angle
un point de l'anneau. Il fait un angle 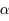 avec le premier axe (même origine que l'angle
avec le premier axe (même origine que l'angle 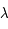 ).
).
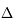 de
de 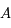 à
à 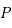 .
.
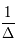 en se limitant aux termes de degré 2 au plus en
en se limitant aux termes de degré 2 au plus en 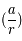 .
.
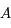 variant le long de l'anneau. C'est-à-dire, il faut intégrer cette expression par rapport à
variant le long de l'anneau. C'est-à-dire, il faut intégrer cette expression par rapport à 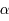 qui varie de
qui varie de 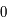 à
à 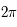 .
.
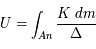 .
.
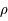 la masse linéique, on peut écrire
la masse linéique, on peut écrire 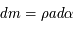 . L'anneau est homogène donc
. L'anneau est homogène donc 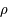 est constant.
est constant.
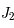 , donner le rayon de l'anneau correspondant au potentiel terrestre. On donne
, donner le rayon de l'anneau correspondant au potentiel terrestre. On donne 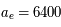 km.
km.
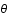 et
et 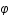 sont choisis comme nuls. On peut donc simplifier la métrique:
sont choisis comme nuls. On peut donc simplifier la métrique:
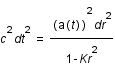 soit
soit 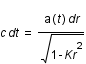 .
.
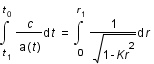
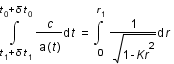
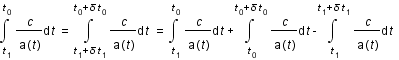
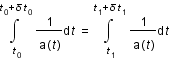
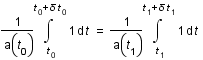
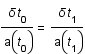
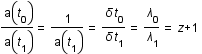
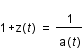
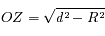 . On en déduit que:
. On en déduit que:
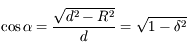 .
.
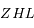 rectangle en
rectangle en 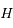 on a:
on a:
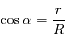 .
On en déduit que:
.
On en déduit que:
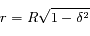 .
.
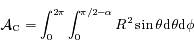 ,
où
,
où 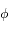 est l'angle
est l'angle 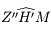 et
et 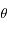 l'angle
l'angle 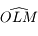 avec
avec 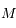 un point de la calotte,
un point de la calotte, 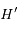 son projeté orthogonal sur la droite
son projeté orthogonal sur la droite 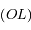 et
et 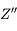 le point de la droite
le point de la droite 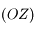 dont la projection orthogonale sur
dont la projection orthogonale sur 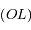 est
est 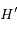 .
.
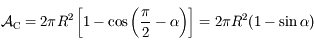 .
C'est-à-dire:
.
C'est-à-dire:
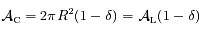 .
.
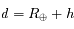 , ainsi
, ainsi 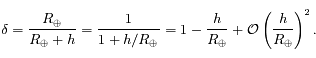 Ainsi
Ainsi 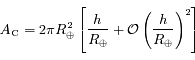 .
.
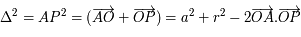
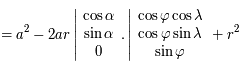
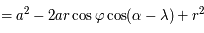
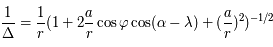
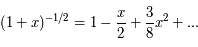
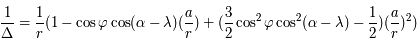
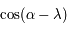 , intégré entre
, intégré entre 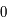 et
et 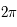 , est nul.
, est nul.
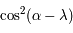 , la valeur de l'intégrale est
, la valeur de l'intégrale est 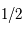 (il suffit de linéariser).
(il suffit de linéariser).
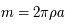 (masse totale de l'anneau) et en notant
(masse totale de l'anneau) et en notant 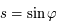 , on obtient:
, on obtient:
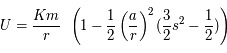
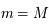 , puis en identifiant les 2 expressions, on obtient
, puis en identifiant les 2 expressions, on obtient 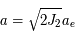 . Ce qui donne 297 km.
. Ce qui donne 297 km.