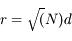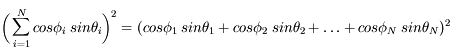
Si on développe le premier terme, on voit que :

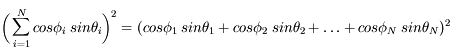
\bigg(\sum_{i=1}^{N}cos \phi_{i} \; sin \theta_{i}\bigg)^2 = (cos \phi_{1} \; sin \theta_{1} + cos \phi_{2} \; sin \theta_{2} +\ldots + cos \phi_{N} \; sin \theta_{N})^2

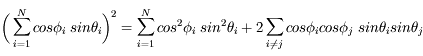
\bigg(\sum_{i=1}^{N}cos \phi_{i} \; sin \theta_{i}\bigg)^2 = \sum_{i=1}^{N}cos^2 \phi_{i} \; sin^2 \theta_{i} +2\sum_{i\ne j} cos \phi_{i} cos \phi_{j} \; sin \theta_{i} sin \theta_{j}

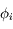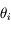Les directions \phi_{i} et \theta_{i} étant aléatoires et indépendantes, le second terme s'annule en moyenne. On a donc :

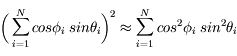
\bigg(\sum_{i=1}^{N}cos \phi_{i} \; sin \theta_{i}\bigg)^2 \approx \sum_{i=1}^{N}cos^2 \phi_{i} \; sin^2 \theta_{i}

Les deux autres termes intervenant dans la distance donnent de façon similaire :

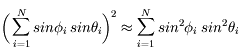
\bigg(\sum_{i=1}^{N}sin \phi_{i} \; sin \theta_{i}\bigg)^2 \approx \sum_{i=1}^{N}sin^2 \phi_{i} \; sin^2 \theta_{i}

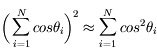
\bigg(\sum_{i=1}^{N}cos \theta_{i}\bigg)^2 \approx \sum_{i=1}^{N}cos^2 \theta_{i}

Si N est suffisamment grand, on a donc :

r^2 = d^2 \biggl[\sum_{i=1}^{N}cos^2 \phi_{i} \; sin^2 \theta_{i} + \sum_{i=1}^{N}sin^2 \phi_{i} \; sin^2 \theta_{i} + \sum_{i=1}^{N} \; cos^2 \theta_{i}) \biggl] soit

r^2 = d^2 \sum_{i=1}^{N}[(cos^2 \phi_{i}+sin^2 \phi_{i}) \; sin^2 \theta_{i} + \; cos^2 \theta_{i}] ou encore

r = \sqrt(N)d