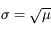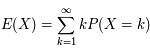
Si X est une variable aléatoire discrète suivant une loi de Poisson, sa valeur moyenne s'écrit :

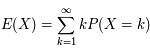
E(X) = \sum_{k=1}^{\infty} kP(X=k)

On note ici 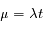\mu = \lambda t

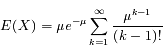
E(X) = \mu e^{-\mu} \sum_{k=1}^{\infty}\frac{\mu^{k-1}}{(k-1)!}

On remarque que la série est le développement de l'exponentielle, il reste :

E(X) = \mu

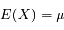
La variance de X s'écrit :

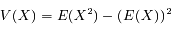
V(X) = E(X^2) - (E(X))^2

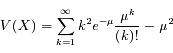
V(X) = \sum_{k=1}^{\infty} k^2 e^{-\mu}\frac{\mu^{k}}{(k)!} - \mu^2

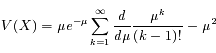
V(X) = \mu e^{-\mu} \sum_{k=1}^{\infty} \frac{d}{d\mu}\frac{\mu^{k}}{(k-1)!} - \mu^2

V(X) = \mu e^{-\mu} \frac{d}{d\mu}[\mu e^{\mu}] - \mu^2

V(X) = \mu

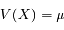
D'où l'écart-type : \sigma = \sqrt{\mu}